¶ Final Presentation
¶ Roadmap Overview
The proliferation of AI technologies, with machine learning at its core, has rapidly accelerated, becoming vital for society. However, conventional computing may approach technological limits in processing the continually growing data volumes with speed and accuracy, especially with advancements in sensor technology. Consequently, "quantum machine learning," which merges the high-speed data processing capabilities of "quantum computing" with "machine learning," is garnering attention for the future.
Quantum machine learning (QML) involves algorithms designed for execution on quantum computers, which operate on principles distinct from classical computers. Consequently, machine learning algorithms for classical computers can't be directly implemented on quantum ones. To utilize QML, algorithms must be adapted to the unique operational principles of quantum computers, a process more complex than typical porting across different operating systems or programming languages. Successful adaptation doesn’t ensure that a quantum computer will outperform its classical counterpart with the adapted algorithm. A quantum algorithm must demonstrably outperform its classical version to be considered valuable, a superiority known as quantum transcendence.
Quantum Machine Learning (QML) intertwines quantum computing and machine learning, presenting a novel approach to handling computational tasks and data processing. Quantum computers, utilizing quantum bits (qubits), operate fundamentally differently from classical computers, which use classical bits (Bit) that represent either "0" or "1". Qubits, on the other hand, can represent both "0" and "1" simultaneously through a phenomenon known as superposition. Various types of qubits, such as "superconducting qubits" and "optical qubits," achieve superposition differently, impacting the theory and apparatus used in calculations.


¶ Types of QML
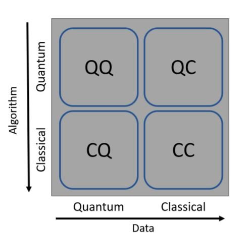
Machine Learning (ML) can be categorized based on the nature of the data and the algorithm used, whether classical or quantum. If either or both the data and algorithm are quantum-based, as illustrated in the preceding figure, the computation is deemed to involve quantum computing, labeled as QQ, QC, or CQ. While this classification is not rigid and several hybrid algorithms exist, we will adhere to this categorization throughout the paper. In certain instances, for example, only the optimization task is performed by a quantum processor, while the remaining processes utilize a classical one.
QML is gaining traction due to its potential to process large data volumes at high speeds, especially in the era of Noisy Intermediate-Scale Quantum (NISQ) computers. NISQ computers, while susceptible to noise and errors, have found a niche in QML due to the latter's tolerance for minor errors and noise. In some instances, qubit fluctuations due to noise can even have a positive impact on certain machine learning algorithms. In the realm of NISQ, Quantum Machine Learning can be considered a viable application due to its inherent tolerance for some level of errors and noise, given that ML algorithms are generally designed assuming the presence of noise and do not require absolute precision. Interestingly, NISQ, with its intrinsic noise, is relatively less prone to overfitting compared to classical computers. Techniques like "quantum circuit learning" (QCL) exhibit characteristics that make them less susceptible to overfitting than classical computers and can achieve high performance with smaller circuits. However, noise, while sometimes beneficial, is fundamentally a hurdle. The "quantum-classical hybrid" NISQ computer was developed to enhance versatility, utilizing a classical computer for calculations where noise is undesirable. This hybrid approach can handle classical and quantum data simultaneously, allowing "complex information" in the quantum world to be expressed directly using qubits, while tasks requiring rigorous and "complex calculations" can be computed using classical bits.
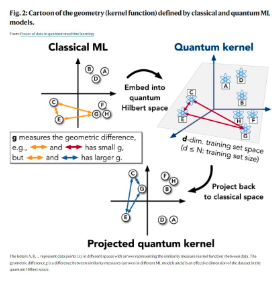
In some paper, the authors devised the quantum kernel method and the projected quantum kernel method as quantum algorithms corresponding to the classical kernel method, and compared their prediction performance. As a result, they proved that the quantum algorithm outperforms the classical algorithm under certain conditions (large model size and large geometric differences.

– File missing when checked in Oct 2025
Quantum deep learning techniques include quantum CNN, hybrid CNN, and quantum RNN. The report also presents research cases where quantum techniques are used to solve natural language processing problems, including the use of quantum techniques to classify hate speech. Quantum machine learning, which can process multiple states simultaneously by superposition, has the potential to significantly shorten the process of learning large amounts of data and trial-and-error in a given environment, which are the characteristics of classical machine learning. Furthermore, quantum machine learning is expected to extract features from complex events that have been difficult to solve with classical machine learning.
¶ Diverse Applications Across Machine Learning Domains
- Supervised Learning: QML in supervised learning explores embedding classical data into quantum spaces, facilitating easier class separation by hyperplanes, akin to classical support vector machines. The embedding is achieved through quantum circuits, utilizing single and multi-qubit gates, and despite being effective on smaller datasets, it theoretically could embed significantly larger amounts of classical information with larger qubit circuits.
- Unsupervised Learning: The application of QML in unsupervised learning, especially in clustering algorithms, involves using quantum-based optimization schemes in classical algorithms to solve problems like the MAXCUT problem on synthetic datasets. Furthermore, Quantum Generative Adversarial Networks (QGANs) and Variational Autoencoders (VAEs) are being explored, with the latter potentially benefiting from replacing simple priors with more complex distributions sampled from a quantum device.
- Reinforcement Learning: QML is also being generalized to solve problems in reinforcement learning, such as the quantum maze problem, where the maze's state evolution is quantum in nature. This approach could optimize the transport of energy and information over complex networks and enhance the development of QML and Noisy Intermediate Scale Quantum (NISQ) technologies.
¶ Challenges and Future Prospects
Despite the promising prospects, QML is still in its nascent stages, with current systems being resource-intensive and often showing subpar performance compared to classical ML systems. The development of QML systems that are deployable in real-life scenarios necessitates substantial effort and research. The theoretical prospects of QML are numerous, but practical implementation is contingent upon overcoming challenges related to quantum computing hardware, algorithm development, and ensuring that quantum versions of algorithms demonstrably outperform their classical counterparts.
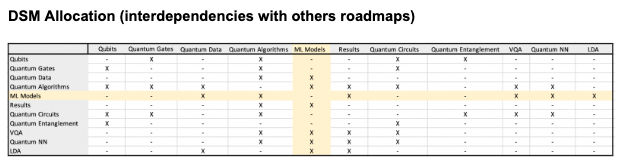
¶ Design Structure Matrix (DSM)

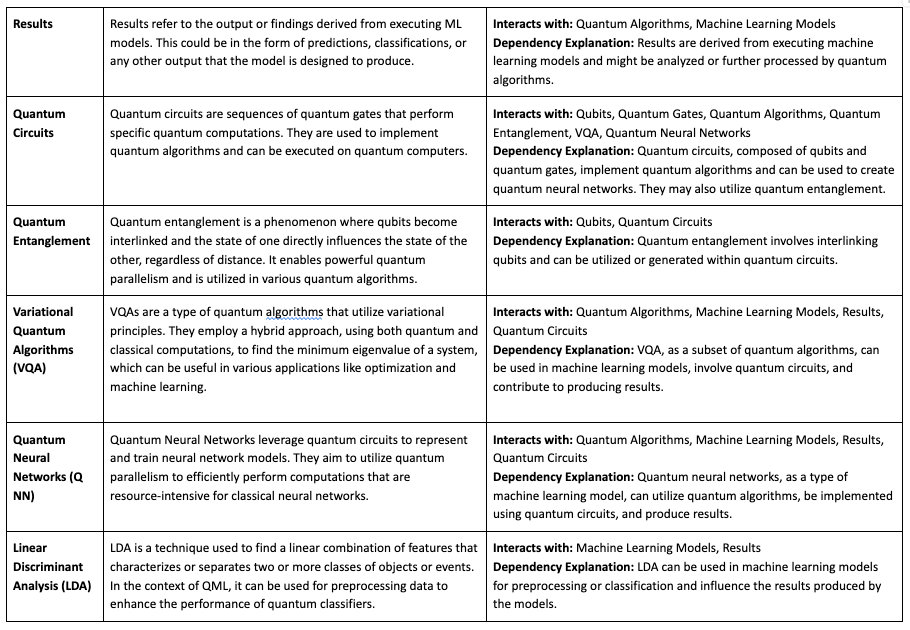
¶ Roadmap using OPM
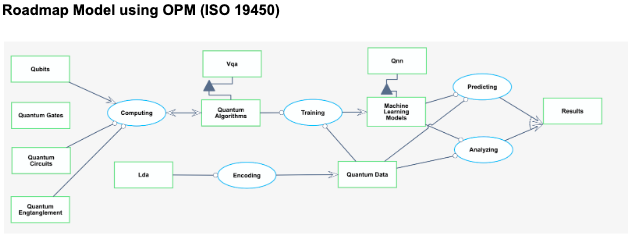
- Sequence Diagram Structure:
- Qubits and Quantum Gates interact to perform computations.
- Quantum Data is encoded, possibly using LDA, to be utilized in quantum computations.
- Quantum Algorithms, which might involve VQA, utilize Quantum Data and are implemented using Quantum Circuits.
- Quantum Circuits utilize Quantum Gates and may leverage Quantum Entanglement.
- ML Models, which might involve Q NN, utilize Quantum Algorithms to perform training and predictions, producing Results.
¶ Figures of Merit (FOM's)
¶ FOM's for Quantum Machine Learning
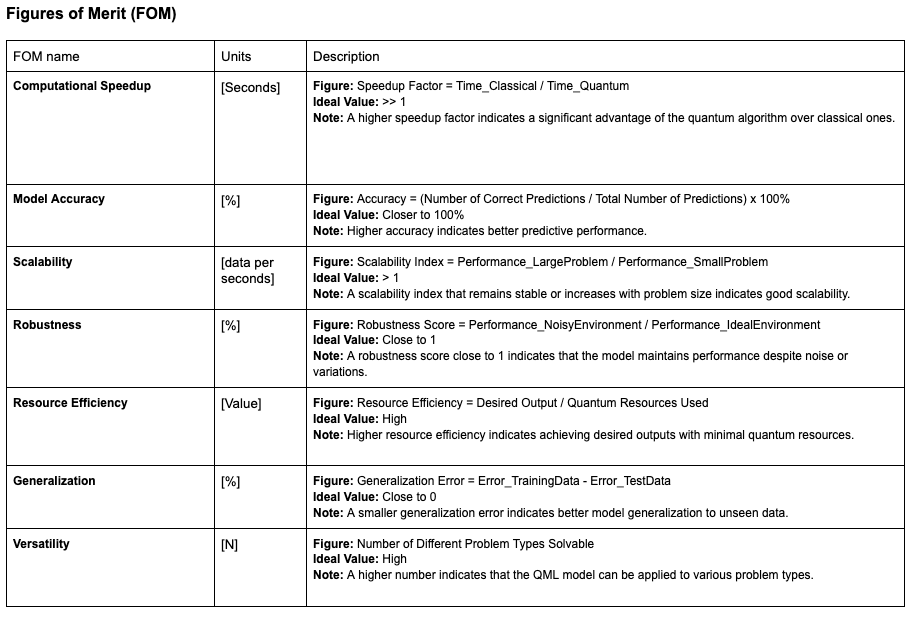
Error creating thumbnail: File missing – File missing when checked in Oct 2025
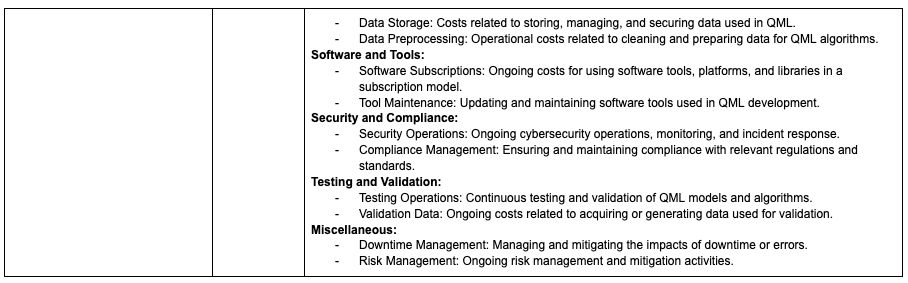
¶ FOM's for Quantum Computing Hardware
Error creating thumbnail: File missing – File missing when checked in Oct 2025
¶ Alignment with "Company" Strategic drivers
The "Company" is a privately held Quantum Computing services company with a mission to bring to market a Quantum Machine Learning SaaS (Software-as-a-service) product. To achieve this mission, the company has to develop best in class Quantum Computing hardware via a hybrid of off the shelf purchases and in-house development. This hardware will then power our cutting edge Quantum Machine Learning algorithms for a variety of B2B (business-to-business) use cases. The table below shows our main strategic drivers and the company's alignment to them so far:

¶ Position of Company vs. Competition: FOM charts
The table below summarizes the various Quantum Computing Hardware off-the-shelf options we either have to compete with or have at our disposal for purchase:
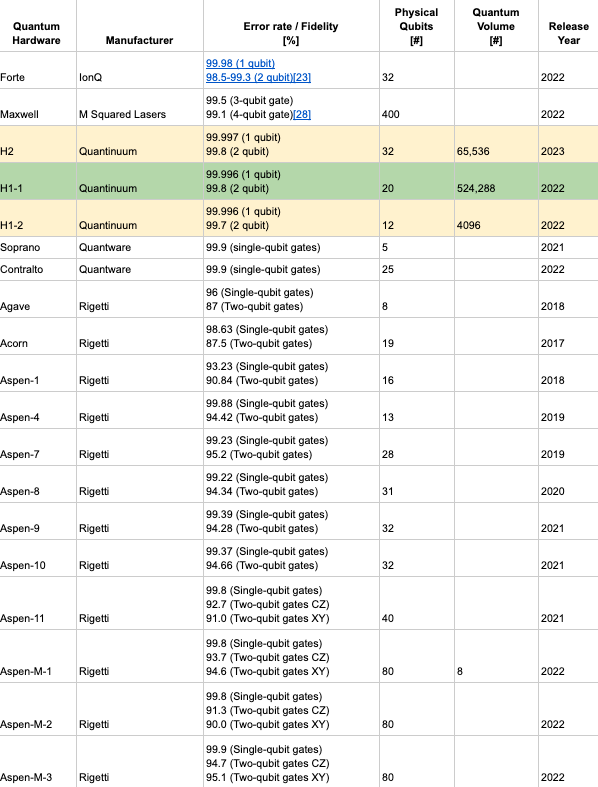
The table above is a subset of the table at: https://en.wikipedia.org/wiki/List_of_quantum_processors#Circuit-based_quantum_processors. We are only considering commercially available hardware and/or SaaS platforms that we can build our QML service on.
The H1-1 from Quantinuum is currently our front-runner quantum computing hardware solution to adopt in terms of balancing between fidelity and number of physical qubits (expressed as a high Quantum Volume). Pricing data is uncertain and thus presents a challenge in terms of developing a financial model for our SaaS offerings. It is therefore somewhat uncertain what we can charge for our QML algorithms as a service - this will be highly dependent on use cases and how big of a problem we are solving for our clients.
¶ Technical Model: Morphological Matrix and Sensitivity Analysis
¶ Morphological Matrix
To better understand our decision for the H1-1 device, we have designed a morphological matrix to more clearly delineate why we chose the device (highest Quantum Volume of the options from Quantinuum). See below:
Error creating thumbnail: File missing – File missing when checked in Oct 2025
¶ Sensitivity Analysis
The best developed mathematical model for the performance of a Quantum Computer is the Quantum Volume (QV) metric defined by IBM. This equation relates two key Figures of Merit (FOM’s) for a quantum computer, number of qubits and error rate, both of which are essential for characterizing how performant a quantum computer is. The equation is:
Error creating thumbnail: File missing – File missing when checked in Oct 2025
QV is a unitless measure of performance that is meant to compare the performance of disparate quantum computing architectures and devices using FOM’s that are common to all of them in this nascent industry. Generally, the larger the QV, the more complex the problems a quantum computer can solve. Unlike classical computer buts, Qubits tend to decohere which results in a loss of performance for the computer. Therefore, there is a tradeoff between number of qubits in the computer and how often they decohere, and so a few fault tolerant qubits tend to be more performant than a larger number of noisy, error-prone qubits.
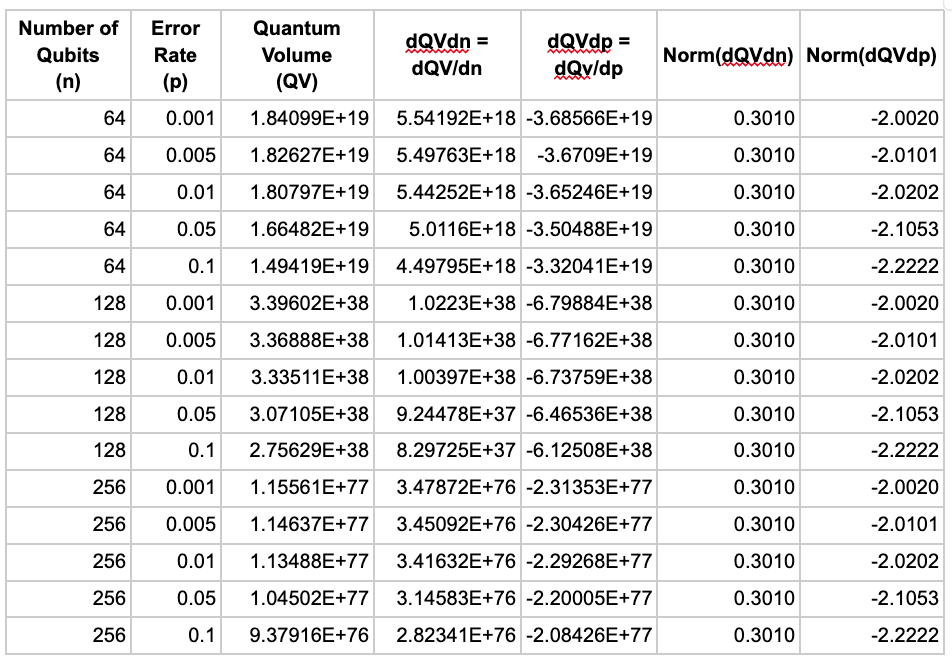
To characterize the sensitivity of the quantum volume to each of the FOM’s, we take the gradient derivative approach with respect to each FOM which yields:
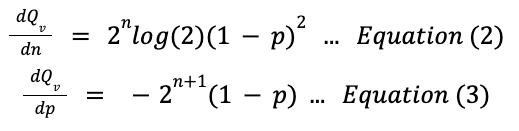
Taking a nominal design point of n=128 Qubits and p=5%, we calculate that:

Therefore, for the chosen nominal design point, we see that the QV is ~3x more sensitive to the incremental change in error rate than it is to the incremental change in the number of qubits. This is a substantial factor, but from what we can see, the differences are within the same order of magnitude. To gain more confidence in this sensitivity analysis, we shall normalize the values of dQvdn and dQvdp based on the corresponding value of Qv for a few design points and producing a table as follows:
What we see in the data is evident from the normalization equations i.e.
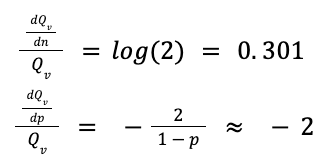
This produces a flame chart as follows:
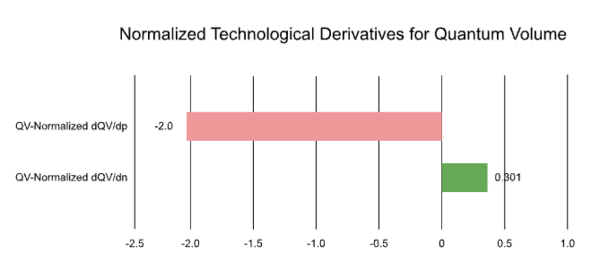
We can therefore conclude that the error rate has a more pronounced effect on the QV of the quantum computer than the number of qubits, which supports the earlier assertion that a few fault tolerant qubits tend to be more performant than a larger number of noisy, error-prone qubits. As the field of Quantum Computing and Quantum Machine Learning grows, It will not be surprising if error rate plays a more crucial role in calculating the computational efficiency of a Quantum Computer system/device in a future governing equation.
For our 2nd FOM, we look at the slightly less complex Stable Qubits (SQ) FOM. This is simply a linear relationship between the number of qubits and the error rate as follows:
Error creating thumbnail: File missing – File missing when checked in Oct 2025
The overall effect of a non-zero error rate is to reduce the number of qubits that are usable for computation from the nominal number of qubits in the quantum computer. Sensitivity analysis for SQ is this more straightforward as follows:
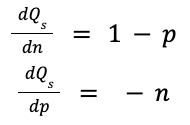
Normalizing each of these sensitivities as before yields:
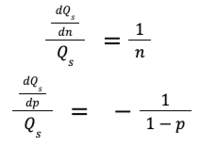
Taking a nominal design point of n=128 Qubits and p=5% as before, we calculate that:

Again we see that the error rate has a more pronounced effect on the SQ of the quantum computer than the number of qubits, upholding the assertion that a few fault tolerant qubits tend to be more performant than a larger number of noisy, error-prone qubits.
¶ Financial Model
¶ Analysis of investment trends of similar companies (ML)
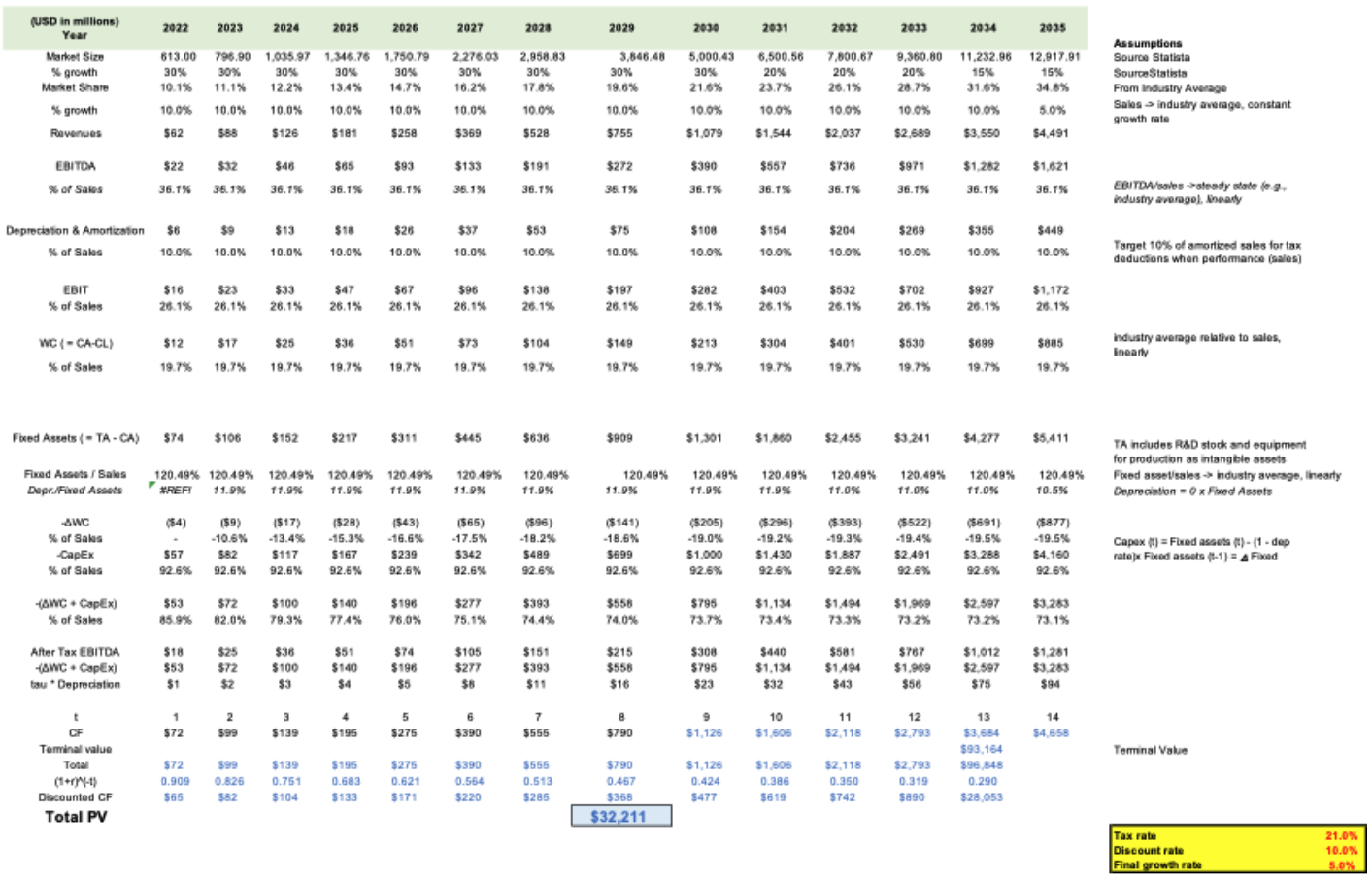
Our team estimated the NPV (Net Present Value) for Quantum Machine Learning development projects. Given that Quantum Machine Learning represents an emerging market, our analysis will focus on investment trends derived from the financial statements of major ML engine developers that currently utilize classical computing in the ML market. This analysis will include average values to mirror the investment patterns in Quantum companies. The data for these leading ML engine developers is sourced from NVIDIA, IBM, Google (Alphabet), and Microsoft. Amazon is excluded from this analysis because its significant retail segment revenues do not align with the trend of pure development investments.
Error creating thumbnail: File missing – File missing when checked in Oct 2025
¶ NPV estimation result
Although the Quantum Machine Learning market is currently highly competitive and witnessing an influx of new entrants, we anticipate that over time, many of these players will be phased out, leaving a few companies to dominate the market share. The target companies in our calculations are projected to adopt investment trends similar to those of the current ML giants, positioning themselves as major players in the Quantum Machine Learning market with an estimated 34.8% market share by 2035. The results of this simulation are presented below, showing an NPV (Net Present Value) of $32,211 million. To calculate the sales, we used the current market size and its Compound Annual Growth Rate (CAGR) forecast provided by Virtue Market Research. The formula is based on the S-curve theory, which assumes that the market's growth rate will gradually decline. Other parameters, as previously mentioned, are derived from the analyzed investment trends and have been incorporated into the formula.
¶ List of R&D Projects (incl. any demonstrator projects)
This section documents a list of Quantum Processor projects by manufacturer and commissioning date as follows:
- Format: Name/Codename,Manufacturer,Release date
- Source: https://en.wikipedia.org/wiki/List_of_quantum_processors#Circuit-based_quantum_processors
List of projects:
- PINE System,Alpine Quantum Technologies,"June 7, 2021"
- Phoenix,Atom Computing,"August 10, 2021"
- N/A,Google,2017
- N/A,Google,Q4 2017 (planned)
- Bristlecone,Google,"March 5, 2018"
- Sycamore,Google,2019
- IBM Q 5 Tenerife,IBM,2016
- IBM Q 5 Yorktown,IBM,
- IBM Q 14 Melbourne,IBM,
- IBM Q 16 Rüschlikon,IBM,"May 17, 2017
- (Retired: 26 September 2018)"
- IBM Q 17,IBM,"May 17, 2017"
- IBM Q 20 Tokyo,IBM,"November 10, 2017"
- IBM Q 20 Austin,IBM,(Retired: 4 July 2018)
- IBM Q 50 prototype,IBM,
- IBM Q 53,IBM,October 2019
- IBM Eagle,IBM,November 2021
- IBM Osprey,IBM,November 2022
- IBM Armonk,IBM,"October 16, 2019"
- IBM Ourense,IBM,"July 3, 2019"
- IBM Vigo,IBM,"July 3, 2019"
- IBM London,IBM,"September 13, 2019"
- IBM Burlington,IBM,"September 13, 2019"
- IBM Essex,IBM,"September 13, 2019"
- IBM Athens,IBM,
- IBM Belem,IBM,
- IBM Bogotá,IBM,
- IBM Casablanca,IBM,(Retired – March 2022)
- IBM Dublin,IBM,
- IBM Guadalupe,IBM,
- IBM Kolkata,IBM,
- IBM Lima,IBM,
- IBM Manhattan,IBM,
- IBM Montreal,IBM,
- IBM Mumbai,IBM,
- IBM Paris,IBM,
- IBM Quito,IBM,
- IBM Rome,IBM,
- IBM Santiago,IBM,
- IBM Sydney,IBM,
- IBM Toronto,IBM,
- 17-Qubit Superconducting Test Chip,Intel,"October 10, 2017"
- Tangle Lake,Intel,"January 9, 2018"
- Tunnel Falls,Intel,"June 15, 2023"
- Harmony,IonQ,2022
- Aria,IonQ,2022
- Forte,IonQ,2022
- Maxwell,M Squared Lasers,November 2022
- Lucy,Oxford Quantum Circuits,2022
- Ascella,Quandela,2022
- Spin-2,QuTech at TU Delft,2020
- Starmon-5,QuTech at TU Delft,2020
- H2,Quantinuum,"May 9, 2023"
- H1-1,Quantinuum,2022
- H1-2 ,Quantinuum,2022
- Soprano,Quantware,July 2021
- Contralto,Quantware,"March 7, 2022"
- Tenor,Quantware,"February 23, 2023"
- Agave,Rigetti,"June 4, 2018"
- Acorn,Rigetti,"December 17, 2017"
- Aspen-1,Rigetti,"November 30, 2018"
- Aspen-4,Rigetti,"March 10, 2019"
- Aspen-7,Rigetti,"November 15, 2019"
- Aspen-8,Rigetti,"May 5, 2020"
- Aspen-9,Rigetti,"February 6, 2021"
- Aspen-10,Rigetti,"November 4, 2021"
- Aspen-11,Rigetti,"December 15, 2021"
- Aspen-M-1,Rigetti,"February 15, 2022"
- Aspen-M-2,Rigetti,"August 1, 2022"
- Aspen-M-3,Rigetti,"December 2, 2022"
- RIKEN,RIKEN,"March 27, 2023"
- Triangulum,SpinQ,September 2021
- Jiuzhang,USTC,2020
- Zuchongzhi,USTC,2020
- Zuchongzhi 21,USTC,2021
- Borealis,Xanadu,2022
- X8 ,Xanadu,2020
- X12,Xanadu,2020
- X24,Xanadu,2020
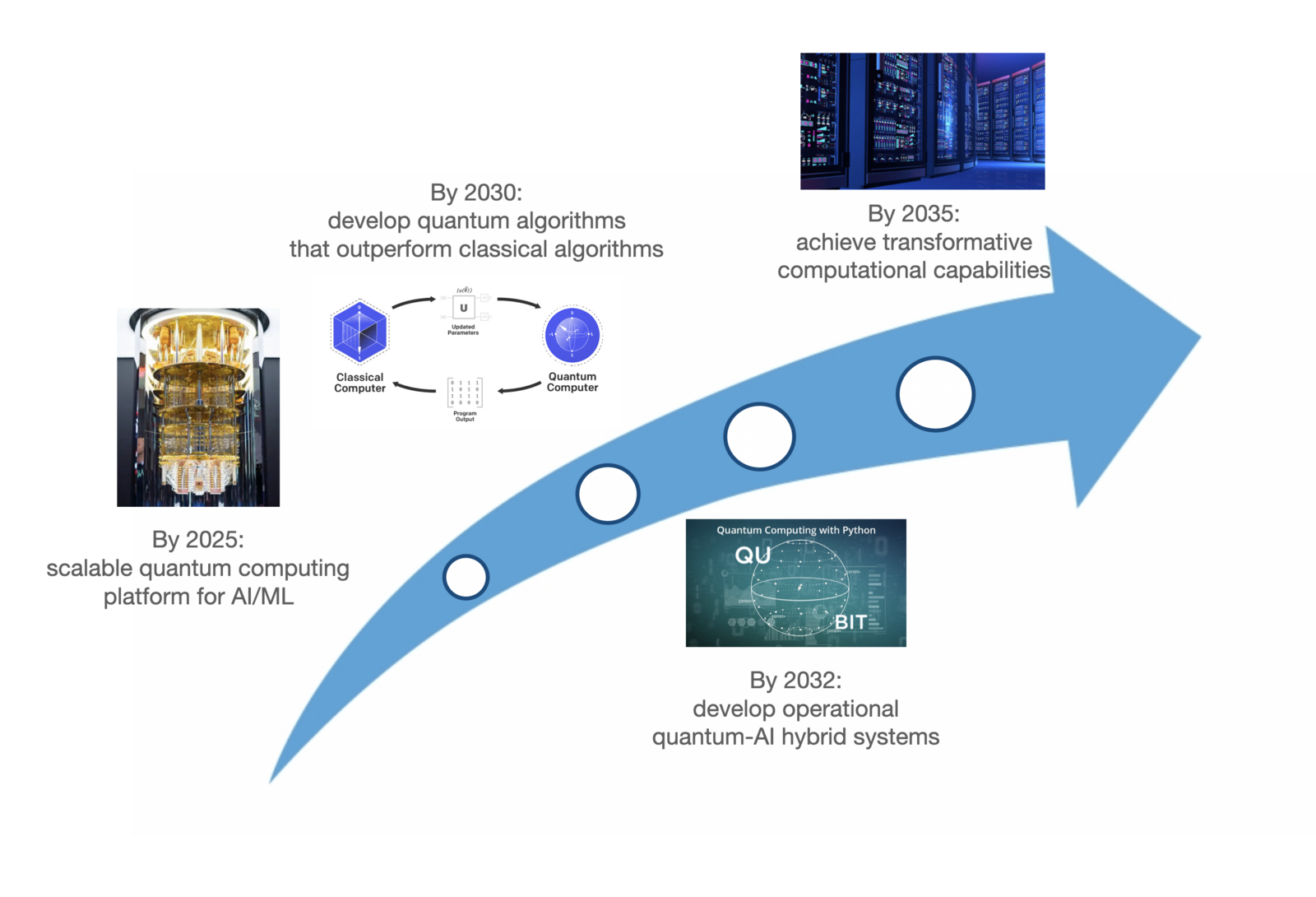
¶ Technology Strategy Statement with “swoosh” chart
Our strategic objective is to pioneer the integration of Quantum Computing in the field of Artificial Intelligence and Machine Learning, aiming to achieve transformative computational capabilities by 2035. Our focus is on harnessing the unparalleled processing power of quantum computers to solve complex AI/ML problems that are currently intractable with classical computing methods. To realize this vision, we will invest in several key R&D initiatives:
- Quantum Algorithm Development: We will concentrate on creating and refining quantum algorithms specifically designed for AI/ML applications. This includes algorithms for quantum machine learning, optimization, and pattern recognition. Our goal is to develop algorithms that can significantly outperform their classical counterparts by 2030.
- Quantum Hardware Advancement: Parallel to algorithm development, we will collaborate with leading quantum technology companies to advance quantum hardware. This will involve enhancing qubit coherence times, quantum error correction, and scalability. By 2025, we aim to have a stable and scalable quantum computing platform suitable for AI/ML experimentation.
- Quantum-AI Hybrid Systems: Recognizing the current nascent stage of quantum computing, we will also focus on developing hybrid systems that leverage both quantum and classical computing strengths. These systems will be crucial in the near term for advancing AI/ML applications and will serve as a bridge to fully quantum solutions.