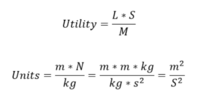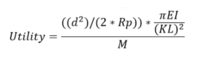Space Booms

Technology Roadmap Sections and Deliverables

This technology's unique identifier is:

• 3SB - Space Boom

This indicates that we are dealing with a “level 3” roadmap at the subsystem level, where “level 1” would indicate a market level roadmap, "level 2" would be at the product level, and “level 4” would be at the component level.

Roadmap Overview

This roadmap is a level 3 (subsystem) assessment of space booms. Space booms are structures used to position space instruments in relationship to the primary mission vehicle. The vehicles are the level 2 (system) for this roadmap and the hardware and software elements of the booms are level 4 (components). Space booms could fall into many L1 ecosystems, but the focus here will be on using space booms as enabling infrastructure on space vehicles. Booms may not seem like glamorous pieces of technology, but they have a glamorous history of enabling space instrumentation by providing the right geometry, relationships, support and protection. On the International Space Station alone, Northrup Grumman's FAST Mast allows the station's solar panels to be extended and retracted as needed, while Canadarm 2 captures incoming resupply vehicles and conducts critical robotic repair on the exterior of the station. Some booms are as simple as a single metal rod, but others are transforming apparatuses that launch in compact forms but can support instruments over great distances once deployed. For this research, primary vehicle and instrument are relative terms; it may be a satellite is the primary vehicle with space boom attached, but the satellite can also be an instrument relative to the Space Shuttle.

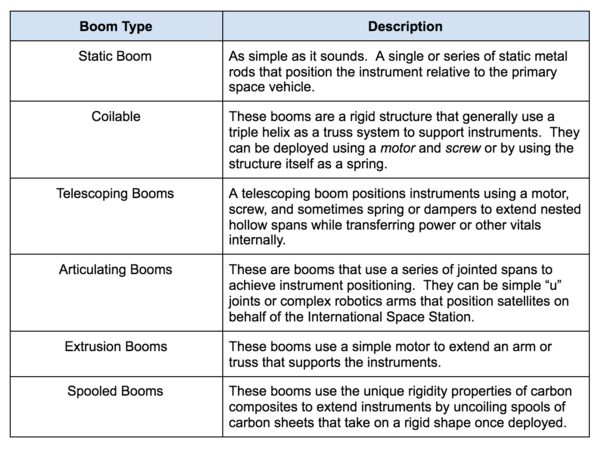
There are several types of booms that have appeared in our research, each with varying degrees of complexity:

There may be other specific types of booms, but these are space industry standards and encompass the vast majority of space booms used since the 1960. This research does not focus on static booms because they are constrained by launch vehicle fairing. The rest of the boom types on the other hand use innovation and technological advances to fit within small spaces, but allow instruments to conduct tests well away from the primary mission vehicle. This leads to a value function for booms: to take up as little space, to use as little mass, and to maintain affordability, allowing the maximization of spacecraft features and instruments.

The research into booms is ongoing, but there is already a celebrity list of booms that are both interesting and demonstrate great engineering. CanadaArms 1 and 2, the Magnetometer Boom that crashed with Cassini into Saturn, and the longest rigid span space structure ever, the Able Engineering ADAM Mast that supported the Space Shuttle Topography Mapping in 2000. From our growing list of research subjects, a reasonably complete list of boom parts is available; enabling a consistent decomposition across the various types. The decomposition is listed in the OPM and allows for Level 4 (component) analysis to be accomplished.

Space booms are not the lead actors for the space movie. However, they are critical infrastructure and enable significant improvements in capability. To make gains in the space boom technology arena means taking advantage of component technology and advanced material sciences to reduce cost, mass, and launch volume to span ratio in order to maximize space mission effectiveness.

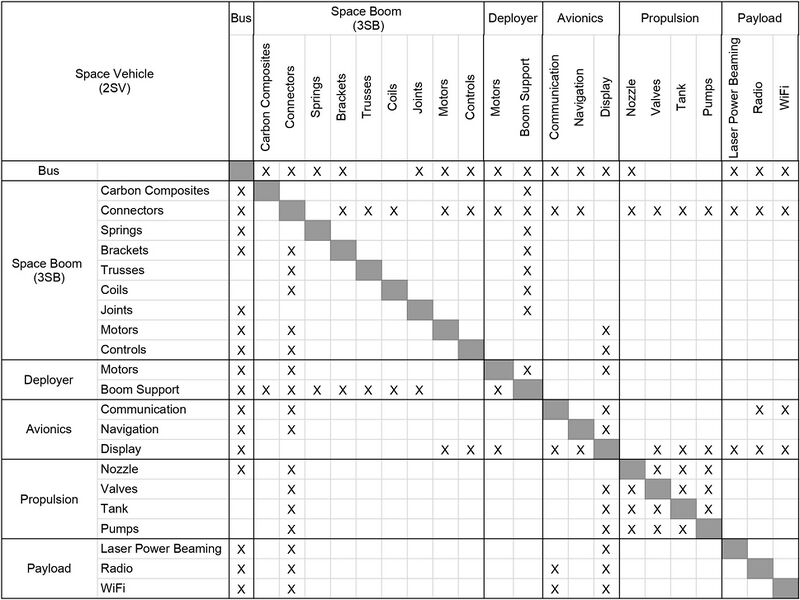
Design Structure Matrix (DSM) Allocation

This DSM shows that space booms are part of the larger space vehicle system, where a space vehicle could be a satellite, a rover, or another type of payload. As a L3 technology, space booms rely on other L3 technologies like propulsion and enable other L3 technologies like payloads. Space booms rely on enabling L4 technology such as carbon composites and controls.

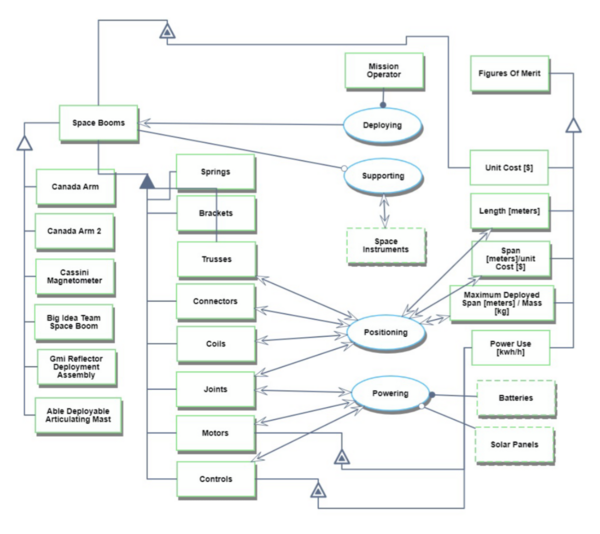
Roadmap Model using OPM

On the left is an Object Process Diagram (OPD), which captures the figures of merit, several examples of space booms, and the main processes and components involved in building and operating a space boom. An Object Process Language (OPL) description of the roadmap scope is auto-generated and shown on the right. It reflects the same content as the previous figure, but in a formal natural language.

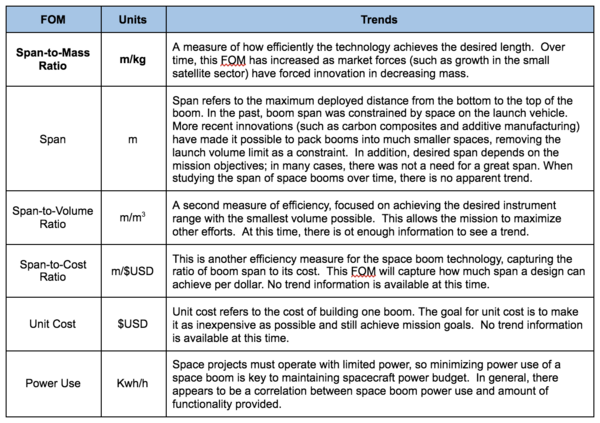
Figures of Merit

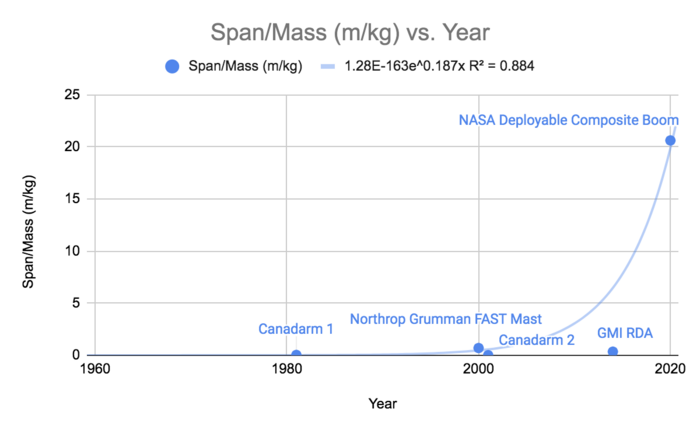
The table below summarizes several figures of merit (FOM) to measure space boom technology. The FOM in bold, span-to-mass ratio, is the primary focus of study.

This figure shows the development of the span-to-mass ratio over time. This shows a significant improvement in recent years by NASA's Game-Changing Development team, which is working on deployable composite booms (DCB).

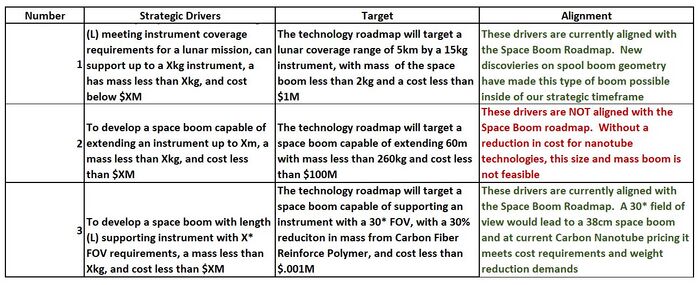
Alignment of Strategic Drivers

Based on the displayed FOMs, our team can define our strategies, set targets for success, and then use our roadmap to determine if they are feasible now or require patience before execution. The below chart depicts the strategies we considered, the targets associated based on roadmap FOMs, and whether or not they are currently viable:

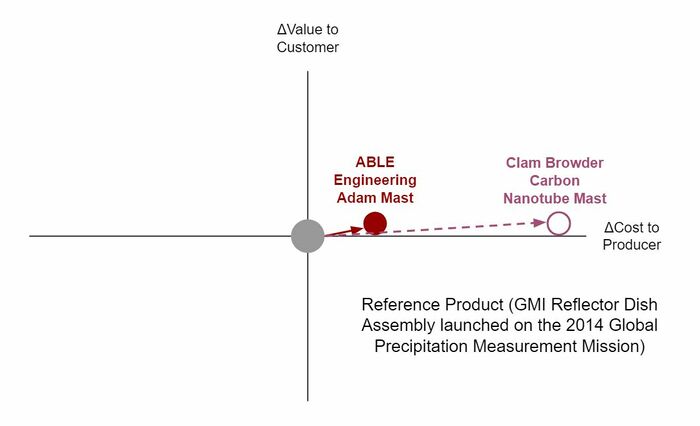
Strategic driver number one is an effort to compete in the commercial composite spoolable boom arena. Given the existing material properties, market costs, and recent NASA research into boom geometry, we believe we can outpace current commercial efforts. Strategic driver number two is an effort to outpace the ABLE Engineering Mast that flew on the Space Shuttle. Its considerable weight makes it incapable of being used on missions without the Space Shuttle, thus creating topographical mapping gaps. Unfortunately, carbon nanotube weight reduction is not offset in this use context by the considerable cost increase. However, Strategic Driver number 3 is asking for to undercut the current weight standards for a short boom. We believe it is accomplishable using Carbon Nanotube Structures, which will take some investment but can still be competitive from a cost position given that it is a relatively small boom application.

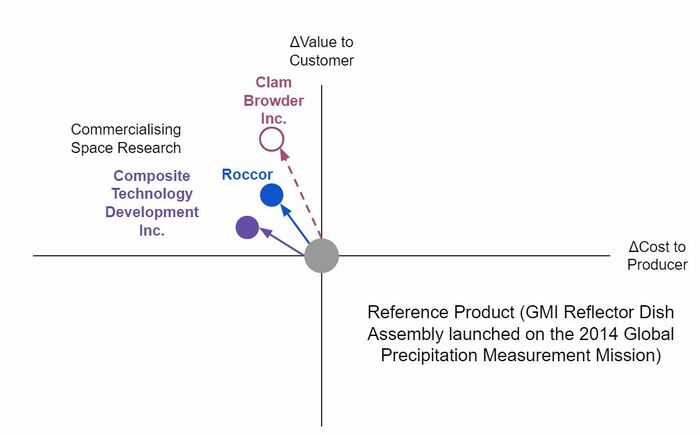
Positioning: Company Versus Competition

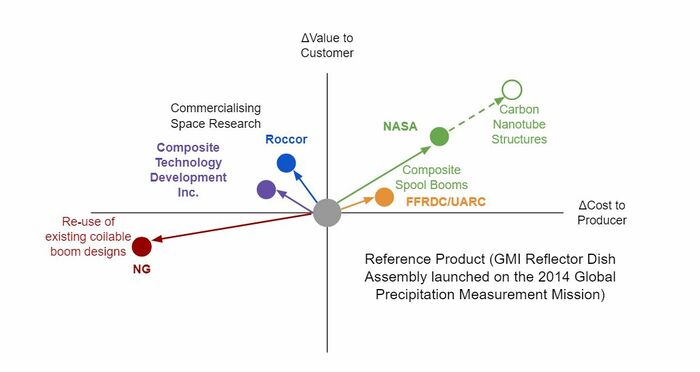
The first step to defining a winning strategy for space boom technology development is to understand the current landscape of companies and government agencies. The following chart highlights the various strategies employed by a couple of distinct groups:

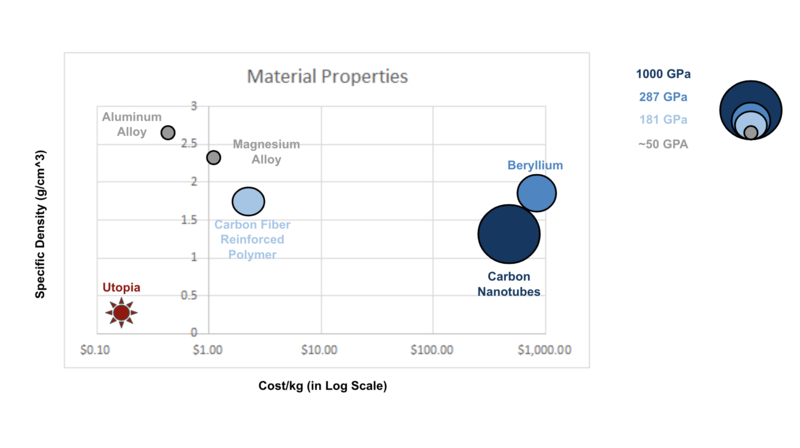
As the chart displays, the strategic space for space booms is highly dependent on whether or not there is government funding associated with space missions. Government funding tends to be focused on novel space exploration that requires unique boom solutions. This drives NASA, the United States Space Force, and supporting research laboratories to accept the additional cost to the producer to gain the added value to customers. These groups are pushing the envelope of material sciences, uncovering optimal geometry, and innovating mechanisms to create compact and light launch profiles. Our team conducted a review of NASA’s Carbon Nanotube Materials for Space Structures and they clearly are targeting it as a lighter and stronger next step. The chart below demonstrates where it currently stands in comparison to existing space materials in terms of cost, density, and stiffness:

The previous chart demonstrates that Carbon Nanotube Structure Technology will both make space structures lighter and better at supporting instruments, but currently only does so at a significant increase in cost.

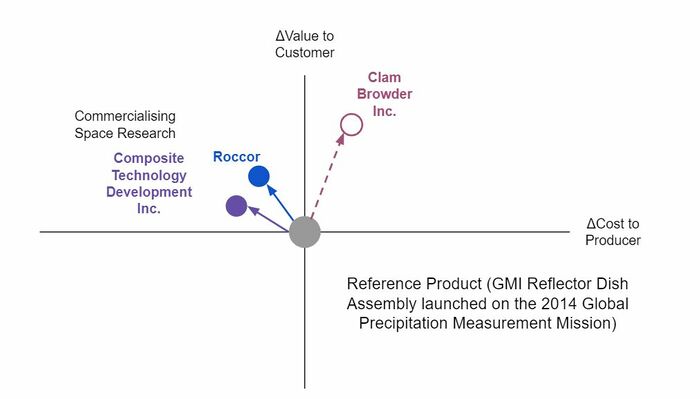
On the commercial side, there are two strategies. One is to try and commercialize, or make profitable, the previously stated novel solutions after they have been successfully demonstrated. Two small space company examples are listed who are working to refine, design for manufacturability, and proliferate a NASA spool boom technology: Roccor and Composite Technology Development (CTD), Inc. The second strategy, favored by large space companies, is to rely on mature, albeit dated technologies. For example, Northrop Grumman has re-used virtually the same coilable boom design, AstroMast, on more than a dozen missions dating back to the 1970’s. [1]

Returning to our strategic drivers the positional comparisons look like this:

Technical Model: Morphological Matrix and Tradespace

In order to understand the feasibility of technical targets for space booms a technical model is required. The first step to building a technical model for space booms is to consider what is “good” for space booms and the environment they operate in. Good in this case is defined as performing their task over the duration of the mission for an affordable cost while adhering to mass and volumetric constraints imposed by the launch vehicle. While cost and durability are relatively easy to understand, the combination of performing its designated mission and fitting inside the rocket fairing poses a challenge for booms. We defined the role of space booms as supporting an instrument in relation to a main body, which brings with it a couple of requirements based on the use context.

The three types of force that space booms will endure while supporting an instrument are compressive loading, torsional forces and angular forces. These often depend on the use case for the system whether it be orbital, lunar, or planetary. The three unique forces could be simultaneously applied, but the assumption for this analysis is that they are mutually exclusive. This creates the requirement to resist forces that may injure the spacecraft or the instrument. Another requirement imposed on space booms is that of length or span as we are defining it for this analysis. Many instruments require a minimum amount of distance from the body given field of view requirements, coverage over a celestial body, or potential for instrument noise. This again depends on the instrument and the use case.

Finally, we must consider the constraints of space systems. Anything we launch into space is constrained in terms of mass by the launch vehicle and volumetrically by the launch fairing. Further constraints can be imposed from the space vehicle itself in terms of mass, volume, and cost budgets. Efficiency is therefore ideal. Gathering these pieces, we begin to develop an idea of utility for a space boom: efficiently achieving the desired span and support requirements. Our analysis assembled a model using these:

Where L = Length of the boom (context dependent minimum length required) [m], F = Force (context dependent minimum force required) [N], and M = Mass of the boom [kg]. For length and force, the technology designer must make a few choices about goals:

• What is the requirement for selecting a length? There are three potential situations:
  • Minimum length needed to clear the field of view (FOV)
  • Length needed to achieve a sufficient coverage range on a celestial body
  • Minimum length needed to prevent interference with instruments that may cause noise
• What are the forces acting on the boom? There are three potential forces that are not mutually exclusive:
  • Compressive Force
  • Torsional Force
  • Angular Force

The next step in analysis is considering a simplified use case. For our analysis we are planning to use our space boom on a lunar mission to vertically support an instrument, therefore we want to achieve sufficient coverage of the lunar surface. This makes defining equations and sensitivity analysis much simpler as the forces expected (compressive loading) and the length requirement (based on range coverage of the Moon) create the utility function together, with mass working to keep them efficient. In this case, critical load refers to the maximum load the space boom can carry when it is used as a tower, which is calculated with Euler’s critical load formula. Range refers to the distance a payload on top of the space boom can see on a planetary surface, which is calculated using Pythagorean theorem. The equation looks like this:

In this composite equation d is the range desired, R_P is the radius of the planetary object, and their combination in this way will yield the required height, or span, for our boom. E starts the portion of the equation focused on compressive loading and is the Young’s modulus of the material. I is the moment of inertia, K is the column effective length factor (a constant based on the end condition of the boom, which is free), L is the length of the boom, and r is the radius of the boom. While acceleration of an object axially on a vertical boom would not be as forceful on the Moon as on earth, this compressive load does serve to compare the maximum capability regardless of planetary body.

A sensitivity analysis of two relevant FOM equations, compressive load and coverage range, will reveal which variables have the greatest impact on our total utility function. To start that analysis, we consider the tradespace for space booms. The various choices available given our use case are listed in the following morphological matrix.

[[]]

Now the two FOMs can be analyzed independently to determine which variables impact them the most. The formula for critical compressive load is:

[[]]

Where E is the Young’s modulus of the material, I is the moment of inertia, K is the column effective length factor (a constant based on the end condition of the boom, which is free), L is the length of the boom, and r is the radius of the boom. In this formula, I was replaced with the moment of inertia for a circle (roughly representative of the boom geometry):

[[]]

For operations on the Moon, this equation would still apply. One consideration to keep in mind is lunar gravity, which is ~⅙ Earth gravity. This would affect the maximum mass that can be supported by the boom.

Calculating the partial derivatives of the critical compressive load with respect to variables E, r and L (K is a constant, so no partial derivative is calculated for it):

[[]]

The design vector of the existing NASA GCD boom is shown in Table 6.

[[]]