Difference between revisions of "Quantum Computers for AI and ML"
(Created page with "Roadmap Overview: The proliferation of AI technologies, with machine learning at its core, has rapidly accelerated, becoming vital for society. However, conventional computing may approach technological limits in processing the continually growing data volumes with speed and accuracy, especially with advancements in sensor technology. Consequently, "quantum machine learning," which merges the high-speed data processing capabilities of "quantum computing" with "machine le...") |
|||
| Line 1: | Line 1: | ||
Roadmap Overview | =Roadmap Overview= | ||
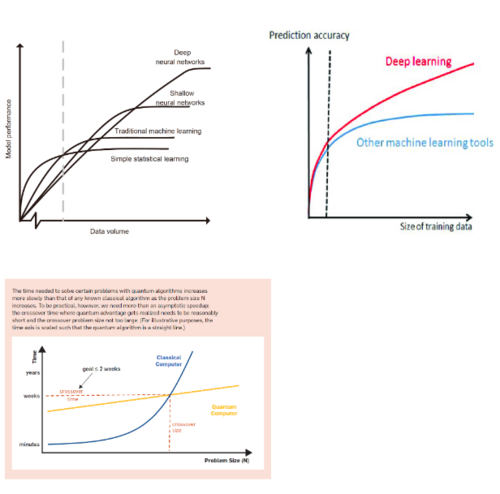
The proliferation of AI technologies, with machine learning at its core, has rapidly accelerated, becoming vital for society. However, conventional computing may approach technological limits in processing the continually growing data volumes with speed and accuracy, especially with advancements in sensor technology. Consequently, "quantum machine learning," which merges the high-speed data processing capabilities of "quantum computing" with "machine learning," is garnering attention for the future. | The proliferation of AI technologies, with machine learning at its core, has rapidly accelerated, becoming vital for society. However, conventional computing may approach technological limits in processing the continually growing data volumes with speed and accuracy, especially with advancements in sensor technology. Consequently, "quantum machine learning," which merges the high-speed data processing capabilities of "quantum computing" with "machine learning," is garnering attention for the future. | ||
[[File:Image-1.png|500px|thumb|center]] | |||
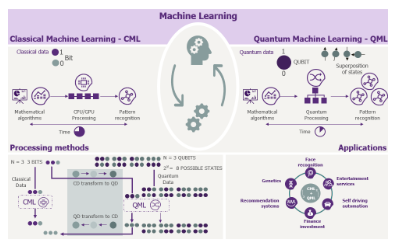
Quantum machine learning (QML) involves algorithms designed for execution on quantum computers, which operate on principles distinct from classical computers. Consequently, machine learning algorithms for classical computers can't be directly implemented on quantum ones. To utilize QML, algorithms must be adapted to the unique operational principles of quantum computers, a process more complex than typical porting across different operating systems or programming languages. Successful adaptation doesn’t ensure that a quantum computer will outperform its classical counterpart with the adapted algorithm. A quantum algorithm must demonstrably outperform its classical version to be considered valuable, a superiority known as quantum transcendence. | |||
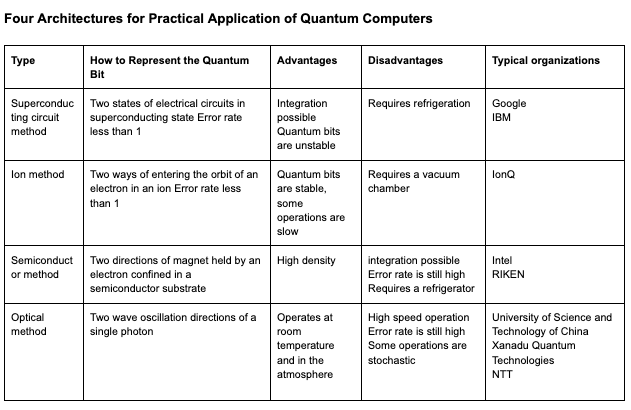
Quantum Machine Learning (QML) intertwines quantum computing and machine learning, presenting a novel approach to handling computational tasks and data processing. Quantum computers, utilizing quantum bits (qubits), operate fundamentally differently from classical computers, which use classical bits (Bit) that represent either "0" or "1". Qubits, on the other hand, can represent both "0" and "1" simultaneously through a phenomenon known as superposition. Various types of qubits, such as "superconducting qubits" and "optical qubits," achieve superposition differently, impacting the theory and apparatus used in calculations. | |||
[[File:Image-2.png|800px|thumb|center]] | |||
[[File:Image-3.png|800px|thumb|center]] | |||
[[File:Image-4.png|800px|thumb|center]] | |||
=Types of QML= | |||
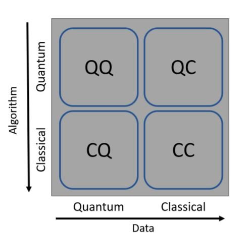
Machine Learning (ML) can be categorized based on the nature of the data and the algorithm used, whether classical or quantum. If either or both the data and algorithm are quantum-based, as illustrated in the preceding figure, the computation is deemed to involve quantum computing, labeled as QQ, QC, or CQ. While this classification is not rigid and several hybrid algorithms exist, we will adhere to this categorization throughout the paper. In certain instances, for example, only the optimization task is performed by a quantum processor, while the remaining processes utilize a classical one. | |||
[[File:Image-5.png|800px|thumb|center]] | |||
QML is gaining traction due to its potential to process large data volumes at high speeds, especially in the era of Noisy Intermediate-Scale Quantum (NISQ) computers. NISQ computers, while susceptible to noise and errors, have found a niche in QML due to the latter's tolerance for minor errors and noise. In some instances, qubit fluctuations due to noise can even have a positive impact on certain machine learning algorithms. In the realm of NISQ, Quantum Machine Learning can be considered a viable application due to its inherent tolerance for some level of errors and noise, given that ML algorithms are generally designed assuming the presence of noise and do not require absolute precision. Interestingly, NISQ, with its intrinsic noise, is relatively less prone to overfitting compared to classical computers. Techniques like "quantum circuit learning" (QCL) exhibit characteristics that make them less susceptible to overfitting than classical computers and can achieve high performance with smaller circuits. | |||
However, noise, while sometimes beneficial, is fundamentally a hurdle. The "quantum-classical hybrid" NISQ computer was developed to enhance versatility, utilizing a classical computer for calculations where noise is undesirable. This hybrid approach can handle classical and quantum data simultaneously, allowing "complex information" in the quantum world to be expressed directly using qubits, while tasks requiring rigorous and "complex calculations" can be computed using classical bits. | |||
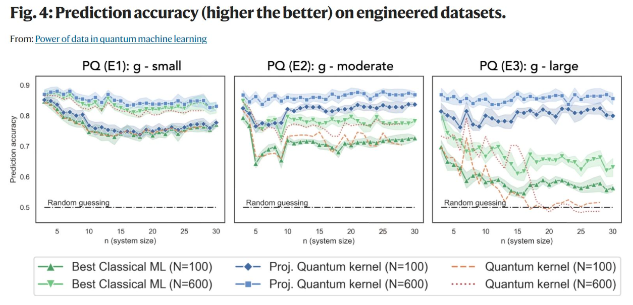
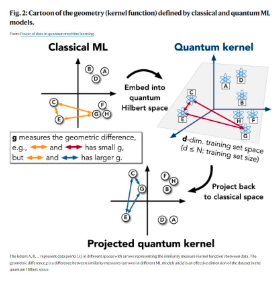
In some paper, the authors devised the quantum kernel method and the projected quantum kernel method as quantum algorithms corresponding to the classical kernel method, and compared their prediction performance. As a result, they proved that the quantum algorithm outperforms the classical algorithm under certain conditions (large model size and large geometric differences. | |||
[[File:Image-6.png|800px|thumb|center]] | |||
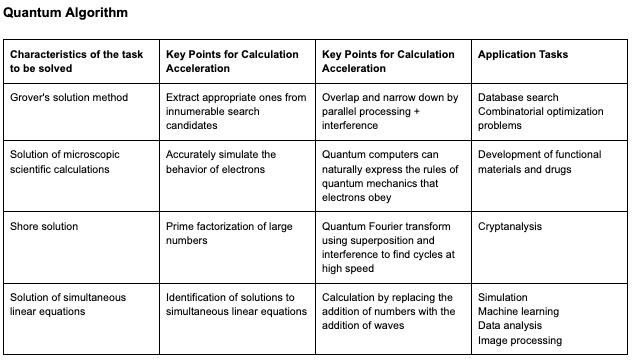
Quantum deep learning techniques include quantum CNN, hybrid CNN, and quantum RNN. The report also presents research cases where quantum techniques are used to solve natural language processing problems, including the use of quantum techniques to classify hate speech. Quantum machine learning, which can process multiple states simultaneously by superposition, has the potential to significantly shorten the process of learning large amounts of data and trial-and-error in a given environment, which are the characteristics of classical machine learning. Furthermore, quantum machine learning is expected to extract features from complex events that have been difficult to solve with classical machine learning. | |||
[[File:Image-7.png|800px|thumb|center]] | |||
=Diverse Applications Across Machine Learning Domains= | |||
* '''Supervised Learning:''' QML in supervised learning explores embedding classical data into quantum spaces, facilitating easier class separation by hyperplanes, akin to classical support vector machines. The embedding is achieved through quantum circuits, utilizing single and multi-qubit gates, and despite being effective on smaller datasets, it theoretically could embed significantly larger amounts of classical information with larger qubit circuits. | |||
* '''Unsupervised Learning:''' The application of QML in unsupervised learning, especially in clustering algorithms, involves using quantum-based optimization schemes in classical algorithms to solve problems like the MAXCUT problem on synthetic datasets. Furthermore, Quantum Generative Adversarial Networks (QGANs) and Variational Autoencoders (VAEs) are being explored, with the latter potentially benefiting from replacing simple priors with more complex distributions sampled from a quantum device. | |||
* '''Reinforcement Learning:''' QML is also being generalized to solve problems in reinforcement learning, such as the quantum maze problem, where the maze's state evolution is quantum in nature. This approach could optimize the transport of energy and information over complex networks and enhance the development of QML and Noisy Intermediate Scale Quantum (NISQ) technologies. | |||
Revision as of 17:23, 12 October 2023
Roadmap Overview
The proliferation of AI technologies, with machine learning at its core, has rapidly accelerated, becoming vital for society. However, conventional computing may approach technological limits in processing the continually growing data volumes with speed and accuracy, especially with advancements in sensor technology. Consequently, "quantum machine learning," which merges the high-speed data processing capabilities of "quantum computing" with "machine learning," is garnering attention for the future.
Quantum machine learning (QML) involves algorithms designed for execution on quantum computers, which operate on principles distinct from classical computers. Consequently, machine learning algorithms for classical computers can't be directly implemented on quantum ones. To utilize QML, algorithms must be adapted to the unique operational principles of quantum computers, a process more complex than typical porting across different operating systems or programming languages. Successful adaptation doesn’t ensure that a quantum computer will outperform its classical counterpart with the adapted algorithm. A quantum algorithm must demonstrably outperform its classical version to be considered valuable, a superiority known as quantum transcendence.
Quantum Machine Learning (QML) intertwines quantum computing and machine learning, presenting a novel approach to handling computational tasks and data processing. Quantum computers, utilizing quantum bits (qubits), operate fundamentally differently from classical computers, which use classical bits (Bit) that represent either "0" or "1". Qubits, on the other hand, can represent both "0" and "1" simultaneously through a phenomenon known as superposition. Various types of qubits, such as "superconducting qubits" and "optical qubits," achieve superposition differently, impacting the theory and apparatus used in calculations.
Types of QML
Machine Learning (ML) can be categorized based on the nature of the data and the algorithm used, whether classical or quantum. If either or both the data and algorithm are quantum-based, as illustrated in the preceding figure, the computation is deemed to involve quantum computing, labeled as QQ, QC, or CQ. While this classification is not rigid and several hybrid algorithms exist, we will adhere to this categorization throughout the paper. In certain instances, for example, only the optimization task is performed by a quantum processor, while the remaining processes utilize a classical one.
QML is gaining traction due to its potential to process large data volumes at high speeds, especially in the era of Noisy Intermediate-Scale Quantum (NISQ) computers. NISQ computers, while susceptible to noise and errors, have found a niche in QML due to the latter's tolerance for minor errors and noise. In some instances, qubit fluctuations due to noise can even have a positive impact on certain machine learning algorithms. In the realm of NISQ, Quantum Machine Learning can be considered a viable application due to its inherent tolerance for some level of errors and noise, given that ML algorithms are generally designed assuming the presence of noise and do not require absolute precision. Interestingly, NISQ, with its intrinsic noise, is relatively less prone to overfitting compared to classical computers. Techniques like "quantum circuit learning" (QCL) exhibit characteristics that make them less susceptible to overfitting than classical computers and can achieve high performance with smaller circuits. However, noise, while sometimes beneficial, is fundamentally a hurdle. The "quantum-classical hybrid" NISQ computer was developed to enhance versatility, utilizing a classical computer for calculations where noise is undesirable. This hybrid approach can handle classical and quantum data simultaneously, allowing "complex information" in the quantum world to be expressed directly using qubits, while tasks requiring rigorous and "complex calculations" can be computed using classical bits.
In some paper, the authors devised the quantum kernel method and the projected quantum kernel method as quantum algorithms corresponding to the classical kernel method, and compared their prediction performance. As a result, they proved that the quantum algorithm outperforms the classical algorithm under certain conditions (large model size and large geometric differences.
Quantum deep learning techniques include quantum CNN, hybrid CNN, and quantum RNN. The report also presents research cases where quantum techniques are used to solve natural language processing problems, including the use of quantum techniques to classify hate speech. Quantum machine learning, which can process multiple states simultaneously by superposition, has the potential to significantly shorten the process of learning large amounts of data and trial-and-error in a given environment, which are the characteristics of classical machine learning. Furthermore, quantum machine learning is expected to extract features from complex events that have been difficult to solve with classical machine learning.
Diverse Applications Across Machine Learning Domains
- Supervised Learning: QML in supervised learning explores embedding classical data into quantum spaces, facilitating easier class separation by hyperplanes, akin to classical support vector machines. The embedding is achieved through quantum circuits, utilizing single and multi-qubit gates, and despite being effective on smaller datasets, it theoretically could embed significantly larger amounts of classical information with larger qubit circuits.
- Unsupervised Learning: The application of QML in unsupervised learning, especially in clustering algorithms, involves using quantum-based optimization schemes in classical algorithms to solve problems like the MAXCUT problem on synthetic datasets. Furthermore, Quantum Generative Adversarial Networks (QGANs) and Variational Autoencoders (VAEs) are being explored, with the latter potentially benefiting from replacing simple priors with more complex distributions sampled from a quantum device.
- Reinforcement Learning: QML is also being generalized to solve problems in reinforcement learning, such as the quantum maze problem, where the maze's state evolution is quantum in nature. This approach could optimize the transport of energy and information over complex networks and enhance the development of QML and Noisy Intermediate Scale Quantum (NISQ) technologies.