Difference between revisions of "Small Launch Vehicles"
| Line 36: | Line 36: | ||
[[File:LaunchChart.PNG|800px]] | [[File:LaunchChart.PNG|800px]] | ||
[[File:Rate.PNG|800px]] | |||
Using a simple linear regression model, we can find a decreasing cost of $-2930.4\$/kg/year$. This means that costs for launch are project to decrease by $2930.40 per year. This is a rough estimate and data is still being collected to make this model more accurate as small launchers are relatively new and data is scarce. | Using a simple linear regression model, we can find a decreasing cost of $-2930.4\$/kg/year$. This means that costs for launch are project to decrease by $2930.40 per year. This is a rough estimate and data is still being collected to make this model more accurate as small launchers are relatively new and data is scarce. | ||
Revision as of 17:47, 1 October 2020
Technology Roadmap Sections and Deliverables
- 1SLV - Small Launch Vehicles
Roadmap Overview
Small launch vehicles (also called "Small launchers" or "Small-lift launch vehicles") are a category of orbital launchers capable of carrying a payload of maximum 2000kg* to LEO (Low Earth Orbit). Half a century ago, many families of launch vehicles have started as small launchers, as prototypes, and led to today's large landscape of heavy launch vehicles (Ariane V, Falcon 9, Soyuz, Delta IV...). Today, the growing market of small satellites (below 500kg) - including, notably, LEO constellations projects and cubesats - pushes towards dedicated small launchers. This trend started in the 90s and considerably accelerated in the 2010s with the development of a broad ecosystem of small launchers startups.
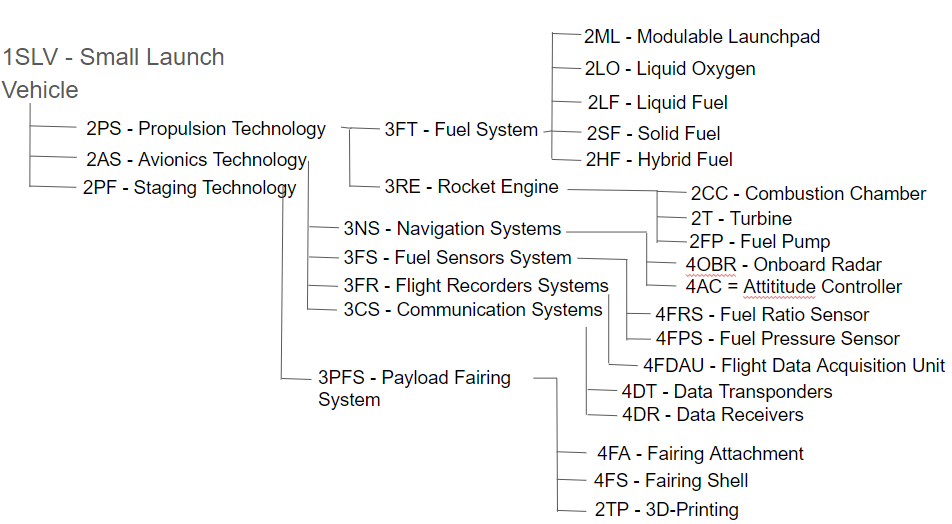
Design Structure Matrix (DSM) Allocation
The DSM demonstrates that such technologies as metal 3-D printing and modulable launchpads are supporting technologies that develop the capabilities of small launchers. Initiatives and development plans for these technologies enhance small launchers by increasing their reusability, launch rate, scheduling flexibility, and reducing their cost per kilogram to launch payloads into orbit.
Roadmap Model using OPM
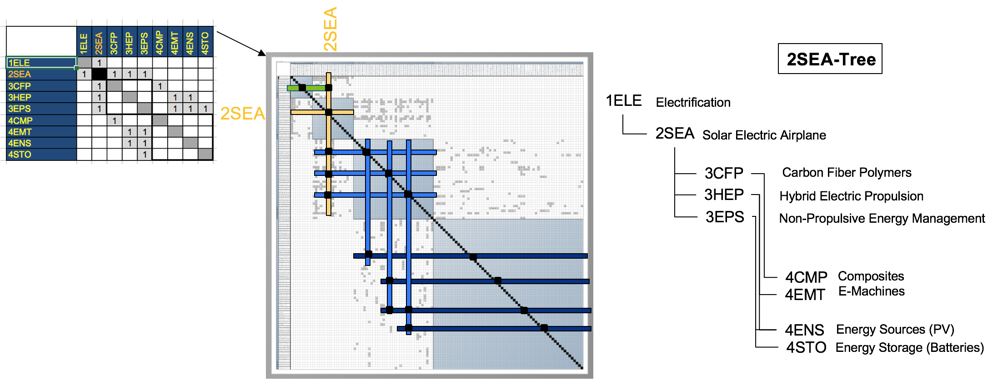
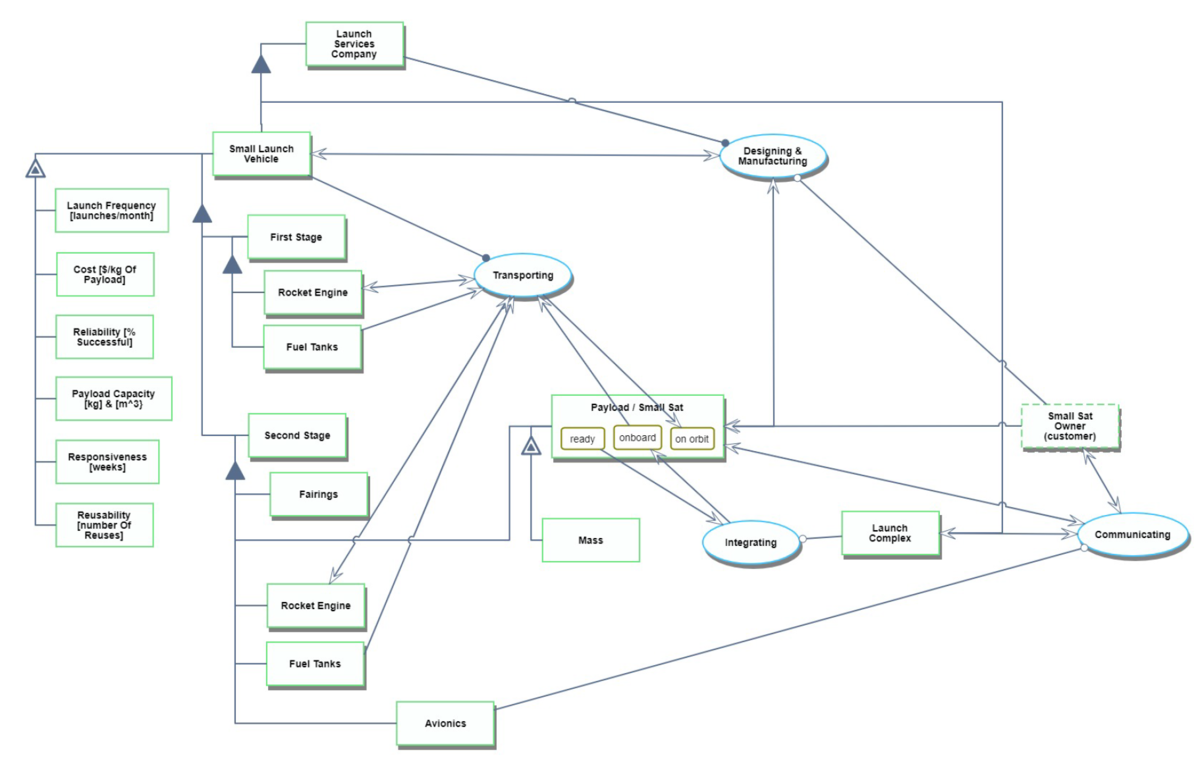
We provide an Object-Process-Diagram (OPD) of the 2SEA roadmap in the figure below. This diagram captures the main object of the roadmap (Solar-Electric Aircraft), its various instances including main competitors, its decomposition into subsystems (wing, battery, e-motor …), its characterization by Figures of Merit (FOMs) as well as the main processes (Flying, Recharging).
An Object-Process-Language (OPL) description of the roadmap scope is auto-generated and given below. It reflects the same content as the previous figure, but in a formal natural language.
Figures of Merit
Figures of Merit (FoM) used to evaluate small launchers are very similar to the FoMs of conventional launch vehicles, but they have redefined the priorities among these. Typical FoMs for small launchers are: Launch Frequency [launch/month], Reliability [$\%$ of successful launches], Payload mass capacity [kg of payload to LEO], Total cost [$\$$], Cost per kg [$\$ /kg$ of payload to LEO], Reusability [Number of reuse cycles], Scheduling flexibility (sometimes called Responsiveness, duration between the launch window and the notification of its flight parameters - orbit, latitude, date...) [weeks or months or years]
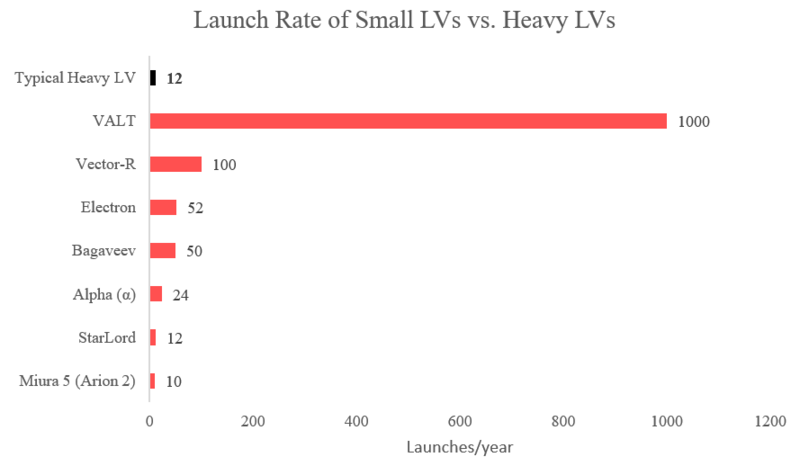
In general, small launcher companies aim for very high launch rates (weekly instead of monthly), high scheduling flexibility (months instead of years), and low launch costs thanks to significant economies of scale enabled by mass production. Some also leverage uncommon launch strategies (balloons, planes, catapults), but here we only include into our scope actual orbital launchers with launching pads on earth or on sea.

THe physics of launchers is governed by the Rocket Equation:
$$\Delta V = v_e \log(\frac{m_0}{m_f})$$
$\Delta V$ is the change of velocity available to the missile
$m_0$ is the initial wet mass
$m_f$ is the (final) dry mass
$v_e$ is the effective exhaust velocity