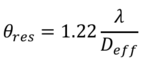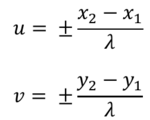Sparse Apertures for Next Generation Optical Space Telescopes

Technology Roadmap Sections and Deliverables

This technology roadmap is identified as follows:

• 2SASOT - Sparse Aperture Space Optical Telescope

This a Level 2 roadmap that evaluates sparse aperture optical telescopes that can achieve larger effective aperture. This feeds into a Level 1 roadmap for next generation space optical telescopes, which includes separate categories like monolithic or segmented telescopes. A Level 3 roadmap would describe the technological progress required to achieve a particular sparse aperture technique (deployable, formation flying, or erecting on-orbit). A Level 4 roadmap would describe individual enabling technologies such as on-orbit alignment metrology, and precision formation flying control algorithms.

Roadmap Overview

The angular resolution of a telescope is proportional to the size of the aperture. The mass and thus cost of space telescopes increases exponentially with aperture diameter. There is a need for systems that can produce the equivalent of a large aperture with low mass. This can be achieved by creating a synthetic aperture using multiple sub-apertures. One method to achieve this is to create a large number of small spacecraft, flying in a formation that creates the synthetic aperture.

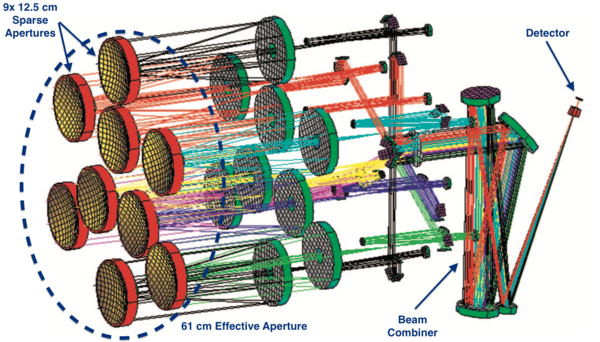
Currently, a sparse aperture space telescope has not yet been fielded. In 2006, Lockheed Martin built a laboratory demonstration of a sparse aperture space telescope, which is depicted in the figure below. Currently, the technology appears be at approximately TRL 4. Research has proven the feasibility of the technology, however, significant technology development must be completed before a space technology demonstration is ready.

DSM Allocation

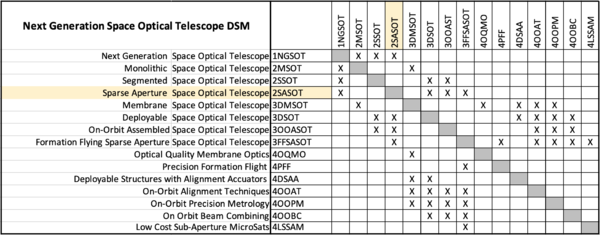
The design structure matrix for space optical telescopes is shown in the figure below. This DSM starts at Level 1.

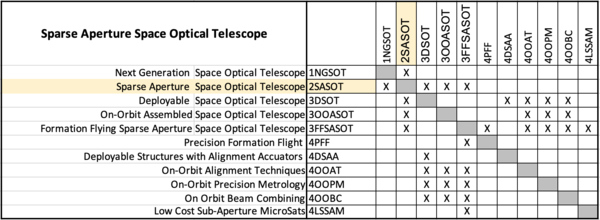
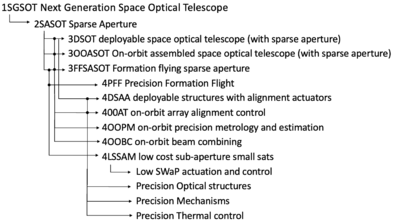
From this top level DSM, we can extract a Level 2 DSM specifically for Sparse Aperture Space Optical Telescopes (SASOT), which is provided below. This matrix can also be view in tree form. Here we can easily see that there are several enabling technologies required to develop SASOTs that are common to all Level 3 instantiations (deployable, on-orbit assembly, formation flying). There are also some technologies that are only feed one Level 3 SASOT, so such as low cost sub-aperture small sats enabling formation flying sparse apertures. Finally, the DSM tree includes some lower level technologies there are also important, but do not have their own specific roadmap identifier at this time.

Roadmap OPM Model

An Object Process Model is presented for a formation-flight synthetic aperture imaging system.  

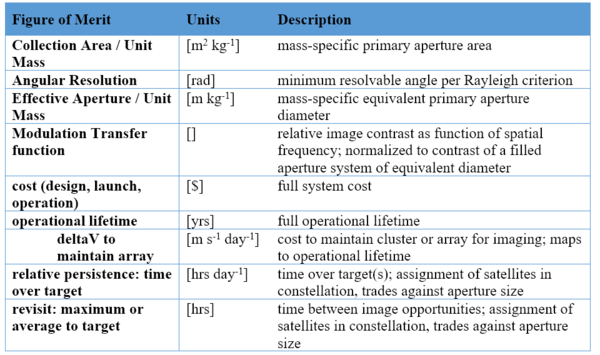
Figures of Merit

One key figure of merit is the mass-specific effective aperture. The figure below shows the progression of this figure of merit over time from early Earth-reconnaissance satellites, to the filled-aperture space telescopes in the past 30 years, to the next generation of synthetic aperture systems that extend the pareto front.

Strategic Drivers and Alignment of Key Figures of Merit

Sparse Aperture Imaging LLC. (SAIL) is a new start-up venture that plans to compete in the rapidly growing Earth imaging marketplace. This market is dominated on the high performance end by vendors such as Lockheed Martin, who have an exquisite sensor with a 1.1 [m] primary mirror on their WorldView-3 satellite. On the opposite side of the spectrum, PlanetLabs competes with constellations of satellites with smaller apertures between 0.9 [cm] - 35 [cm], but provide imagery that is significantly less expensive. In addition, there is also free, publicly available imagery from satellites such as the ESA Sentinel with much lower resolution.

Based on these competitors, SAIL has decided to compete in the medium-to-high resolution arena by out-performing PlanetLabs. However, to keep costs low compared to high performance sensors with monolithic meter-class primaries, SAIL will employ a sparse aperture imaging approach. This roadmap seeks to evaluate the approach that is most suitable for achieving these strategic drivers and hitting the FOM targets laid out in the table below. These targets are grounded in market data from existing systems as well as performance models of the potential gains from sparse aperture systems.

	Strategic Driver	Alignment and Targets
1	Use sparse aperture imaging technology to drive down the effective aperture per kg of the system (which could be a single satellite or multiple flying in formation). This tightly coupled to the total system cost, driver 3.	0.01 [m/kg]: Effective aperture per kg PlanetLabs Dove satellites have one of the highest ratios of effective aperture per kg for imaging satellites because of their small, cubesat form factor, ~ 0.02 [m/kg]. Because mass increases exponentially with aperture, high resolution systems such as WorldView-3 are ~ 0.0004 [m/kg].
2	Provide medium to medium/high resolution data that is able to meet the majority of customer needs using a modular, sparse aperture architecture.	0.75 [mrad] - 1 [mrad]: Angular Resolution* (panchromatic) State of the art satellite imagery able to achieve 0.5 [mrad] panchromatic imagery with private satellites such as WorldView-3. This imagery is sold at a premium. Publicly available imagery from satellites such as Sentinel can provide 12 [mrad] resolution. Relatively in-expensive imagery from PlanetLabs is between 8 - 1.5 [mrad] resolution (RGB).
3	Offer imagery at a competitive price by keeping total system cost low compared to current state-of-the-art systems.	20 [millions of $]: Total System Cost (build and launch of 0.75 [mrad] angular resolution system) Launch costs are a large driver of the total system cost for satellite program. Current imaging satellites with the highest performance are extremely large and therefore require a dedicated launch vehicle, and costs between $601 and $1502 million depending on the launch provider and orbit. SAIL will plan to use smaller satellites that can be launched as ride-shares. This can drive the launch cost down to ~ $5 million (6x - 30x cost reduction). In addition, smaller satellites using cubesat form factors are significantly less expensive. The SkyBox satellites are approximately $5 million3 to build, compared to $650 million4 for WorldView-3

Note*: Ultimately, the ground resolution is a function of the angular resolution and the satellite orbital altitude. Since the orbit can be varied independently (to a large degree), the angular resolution is the best FOM for comparing the capability of the capability of different systems.

References:

1. https://www.airspacemag.com/space/is-spacex-changing-the-rocket-equation-132285884/
2. https://en.wikipedia.org/wiki/Atlas_V#Launch_cost
3. https://www.forecastinternational.com/archive/disp_pdf.cfm?DACH_RECNO=1252
4. https://en.wikipedia.org/wiki/WorldView-3

Technical Model: Morphological Matrix and Tradespace

The Rayleigh Criterion gives the angular resolution as a function of the wavelength and the effective aperture diameter. Therefore, the abstracted FOM in this model is the effective aperture diameter.

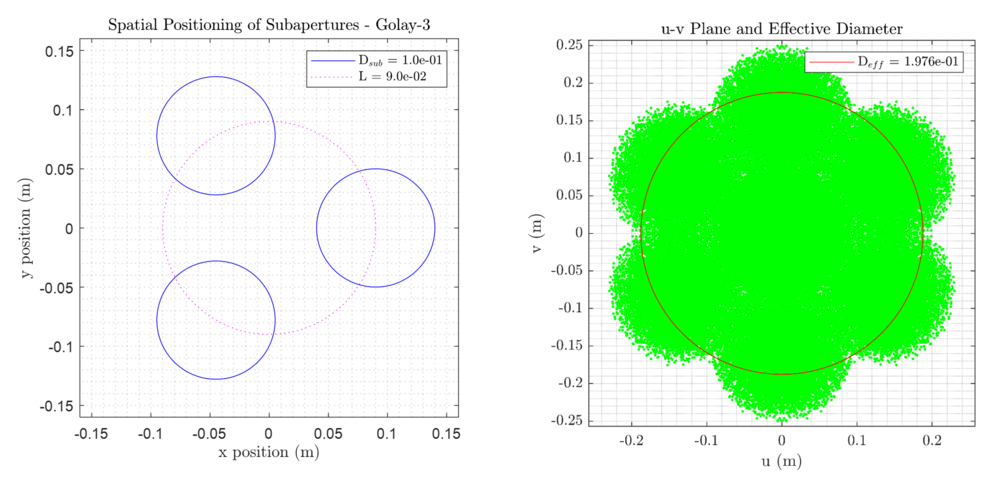
The Rayleigh Criterion assumes that the point sources are resolved as single-peak point spread functions. However, for a non-monolithically filled aperture system, the peaks may not be resolved cleanly. Instead there may be side lobes indicating degraded contrast and thus image quality. These are both functions of the interfered wavelengths. For visible light applications, it is desirous to consider the effective diameter to only include the aperture in which all distances can be interfered. This corresponds to the roots of the modulation transfer function (MTF). A simplified approach is presented in [2] to generate a u-v plane, normalized to the units of the subapertures to calculate an effective aperture diameter within the first root of the MTF (the maximum circumscribed diameter in the u-v plane that contains no singular u-v locations). u-v coordinates are defined for any two points spatially located in the primary aperture imaging plane denoted as (x_1,y_1 ) and (x_2,y_2):

For a given aperture configuration, a Monte Carlo sampling of pairwise points on the physical surfaces of each aperture within the spatial x-y plane can be used to construct the u-v plane. Normalization against the observed wavelength in the u and v equations will produce a result for a wave number of 1. The units of this u-v plane will be in those of the aperture diameter and thus map to an effective aperture relative to the physical x-y plane of the aperture [6]. A numerical edge-search method to find the largest circumscribed area with no sizable intermediate wavelength u-v singularities (empty pockets) is used to determine the effective aperture diameter.

Meinel and Meinel present cost and mass estimates where [4]:

For this analysis, the proportionality for the system mass will be given by:

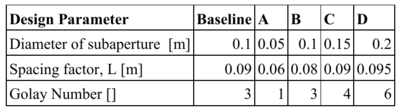
For this sensitivity analysis, 3 design parameters will be considered about the baseline shown:

The results for the numerical Monte Carlo approach to sizing of the effective aperture of the baseline case is shown below:

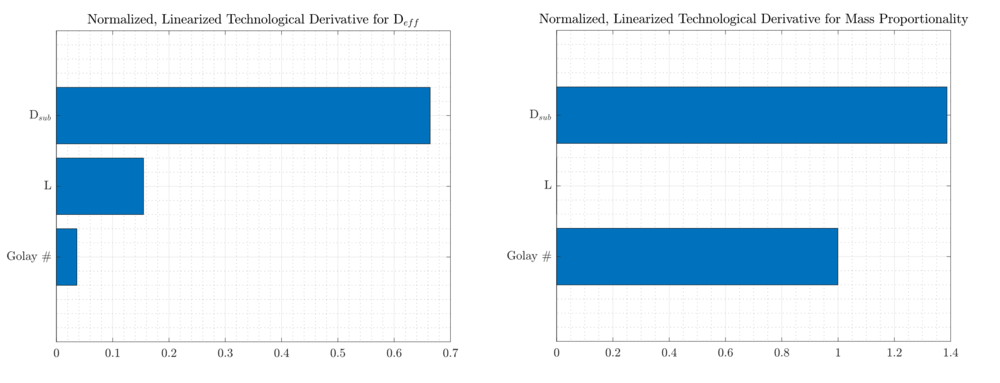
Normalized, univariate sensitivities are shown for stepwise variations from the baseline architecture to the next incremental value for each design parameter.

The normalized sensitivity results show the effect of each univariate perturbation around this baseline. Deff is most strongly affected at this point by the subaperture diameter. This has the corresponding effect of having the highest increase in the mass proportionality term. The net effect of increasing the subaperture diameter for a fixed spacing, is to increase the physical fill factor of the aperture. The ratios of the normalized linearizations indicate that from this point, an increase in the subaperture diameter would be desirable only if the Deff is valued proportionately more than the mass term.

In contrast, perturbation of the L term results in a proportionately low increase in Deff with no penalty to the mass. Therefore, L should be unilaterally increased to move towards the pareto front. However, it should be noted that as L is increased, there is a point where singular regions of the u-v plane will form inside of the inscribed diameter (left figure below). This would indicate that some mid-frequencies are no longer being interfered, and the effective aperture is no longer compact. In this case, a requirement on contrast per the point spread function is needed. Further increase in L will eventually create a continuous region of u-v singularities in all directions (right figure below). This annulus would indicate a new root in the MTF at the diameter of the inner cluster of u-v points. Variation in L is therefore convex.

In this example, the Golay number has a very limited effect since no other terms are varied. In this example, a center aperture is added, but is line-to-line with the other 3 subapertures. The result is that there is only a small effect on the effective aperture diameter, at the cost of 1 additional subaperture of mass. However, it is expected that covariation of the three terms would yield a proportionately greater increase with more subapertures. Furthermore, greater increases necessitate definition of more spacing terms to fully define the arrays.

The sensitivity results represent a linearization of the Jacobian strictly about the given baseline architecture. Changes in the perturbation step size will result in alternate linearizations due to non-linearity. Moreover, sensitivity about a different baseline will yield a vastly different set of linearizations due to the non-linearity. It is also expected that covariation of terms would result in different effects on the FOMs.

Key Publications and Patents

Key Publications:

[1] Golay, Marcel JE. "Point arrays having compact, nonredundant autocorrelations." JOSA 61.2 (1971): 272-273.

• presents optimized, non-redundant point aperture arrays to create effectively large apertures with minimum numbers of elements

[2] Chung, Soon-Jo, David W. Miller, and Olivier L. de Weck. "Design and implementation of sparse-aperture imaging systems." Highly Innovative Space Telescope Concepts. Vol. 4849. International Society for Optics and Photonics, 2002.

• Design and implementation of a Golay-3 synthetic aperture system

[3] Chung, Soon-Jo, and F. Y. Hadaegh. "Swarms of femtosats for synthetic aperture applications." (2011).

• Presents effective aperture calculations for proliferated femtosat clusters; Gaussian arrays, Golay series arrays composed of sub-clusters

[4] Stahl, H. Philip, et al. "Preliminary cost model for space telescopes." UV/Optical/IR Space Telescopes: Innovative Technologies and Concepts IV. Vol. 7436. International Society for Optics and Photonics, 2009.

• Presents several cost and mass models for scaling of space-base telescopes

[5] Dhurandhar, S. V., et al. "Fundamentals of the LISA stable flight formation." Classical and Quantum Gravity 22.3 (2005): 481.

• A proposed 3-element rotating long-baseline interferometer; orbital dynamics solution for low fuel array maintenance

[6] Chung, Soon-Jo. Design, implementation and control of a sparse aperture imaging satellite. Diss. Massachusetts Institute of Technology, 2002.

• Thesis presenting methods for u-v plane analysis and relation to MTF

Key Patents:

1. Hunt, Rafanelli, and Phillip: Full aperture scene synthesis using rotating strip aperture image measurements; 1997; European Patent Office - EP 0 802 425 A3

• This patent presents a novel method to fill the u-v plane through integration of images taken for a rotating strip section of an aperture. This produces an axisymmetric MTF equal to the length of the cross-rotational axis segment of the aperture.
• While not directly a multi-element synthetic aperture, it presents a post-processing method to further extend the effective diameter of a compact imaging system of a Golay series array. Orbital dynamics of a close formation-flight system might already naturally be spinning (e.g., the three-element solution for LISA [5]).

2. Duncan et al., Enhanced Multiple Instrument Distributed Aperture Sensor, 2009, US Patent - US US 7,631,839 B1

• This patent presents an instrument configuration that uses 9 subapertures to produce a large ring aperture. The patent includes the mechanical alignment design to host the 9-element large aperture on a single spacecraft.

3. Auterman, et al., Three Dimensional Interferometric Synthetic Aperture Radar Terrain Mapping with Unambiguous Phase Unwrapping Employing Subset Bandwidth Processing, 1993, US Patent – US 5,260,708

• This patent presents a method for terrain mapping with three-element measurements using interferometry. In particular, it presents a novel method to disambiguate the wave number during interferometry of parallel flight-path swaths. This shows one of the early concepts utilizing interferometry to enhance measurements.