Orbital Launch Vehicles Roadmap

Roadmap Overview

Orbital launch vehicles (LV) are internally propelled vehicles used to carry payloads from Earth’s surface to Earth orbit or beyond. They are powered by rocket engines that generate large amounts of thrust even in vacuum by means of expelling hot gas through a nozzle. The propellants burnt to generate that gas can be liquid or solid (or hybrids) and are stored inside the LV. Most launch vehicles are divided into stages to discard non-used structure and some of them are reusable.

This roadmap will be an L1 roadmap from the point of view of the LVs as a technology that enables the Human race to transport cargo from the surface of the Earth to outer space. ==

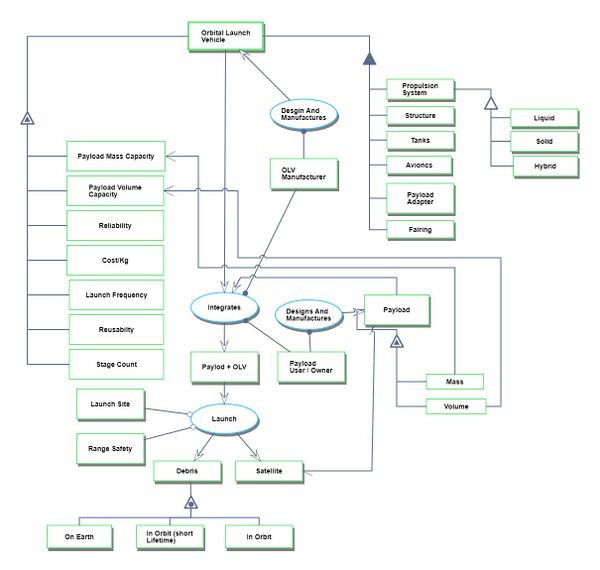
Roadmap model using OPM

The following Object Process Diagram describes the Orbital Launch Vehicle technology point of view for this roadmap. The main object of the diagram is the different launch vehicles, its decomposition into main components/subsystems like propulsion system, structures, tanks, avionics, payload adapters, and the main attributes. Finally, the processes in the lifecycle are described as the integration of the payloads and the actual launch.

Figures of merit

The table below shows a list of FOMs by which Orbital Launch Vehicles can be assessed. The first four (shown in bold) are used to assess the aircraft itself. They are very similar to the FOMs that are used to compare traditional aircraft which are propelled by fossil fuels, the big difference being that 2SEA is essentially emissions free during flight operations. The other rows represent subordinated FOMs that impact the performance and cost of solar electric aircraft but are provided as outputs (primary FOMs) from lower level roadmaps at level 3 or level 4, see the DSM above.

Figure of Merit	Units	Description
Payload to LEO	[Kg/Year]	Payload mass that can be put into a 500 Km circular low earth orbit for a specific launch vehicle every year. This takes into account the production rate of the rockets and, if applicable, the reusability.
Payload to mass Ratio	[Kg/Kg]	A performance FOM on how much mass is the payload of the total mass of the launch vehicle.
Cost per Kg	[USD/Kg]	The (advertised) cost of putting a Kg to the reference orbit when buying an entire rocket. Here it is not considered the effects of brokers and rideshares.
Reliability	[non-dimensional]	Rate of success over total launches per launch vehicle.

Physical principles

In order to put a payload in orbit, an OLV needs to accelerate to a certain velocity in a certain direction at a specific altitude from the center of the Earth. This requirement can be derived from Newton’s Universal Gravitational Law and can be approximated for circular orbits as:

Where G is the universal gravitational constant, M the mass of the Earth and r the distance to the center of the planet of the orbit. So for example, a 500km circular orbit around the Earth will require a velocity of approximately 7.61 km/s or 27405 Km/h. A few more km/s are usually needed to account for atmospheric losses and other non-idealities.

In other to achieve that velocity, OLV uses rockets engines that use a combination of fuel and oxidizers (known as propellants) to create a high-pressure gas that is then accelerated by a converging-diverging nozzle to create thrust.

<math>\Delta v = v_\text{e} \ln \frac{m_0}{m_f} = I_\text{sp} g_0 \ln \frac{m_0}{m_f}</math>

Where ΔV is the change of velocity of the vehicle, m₀ is the initial total mass, including propellant, also known as wet mass, m_f is the final total mass without propellant, also known as dry mass, v_e is the exhaust velocity and is equal to Isp times g₀. Here, Isp is the specific impulse in the dimension of time and is a measure of effectively the rocket use the propellant and g0is standard gravity. In other words, this equation relates the total amount of velocity change that a rocket engine can create on a system by means of the initial and final mass (loss of mass of propellant), the efficiency. When multiple stages are present this equation must be considered for each stage.

So, as ΔV is known, then choosing a propulsion system will define the Isp and this will lead to the ratio of the initial and final mass necessary or which is equivalent to the amount of mass for structure tanks and engines, payload and propellant that is needed.

For example, this table shows some figures of merit of different rocket engines.

OLV	Propellant % of total mass	Payload % of total mass
Saturn V	85	4
Space Shuttle	85	1
Soyuz	91	2

In conclusion, the only FOM that is directly related to a physical principle is the Payload to mass Ratio described above.

Payload to mass Ratio [Kg/Kg]

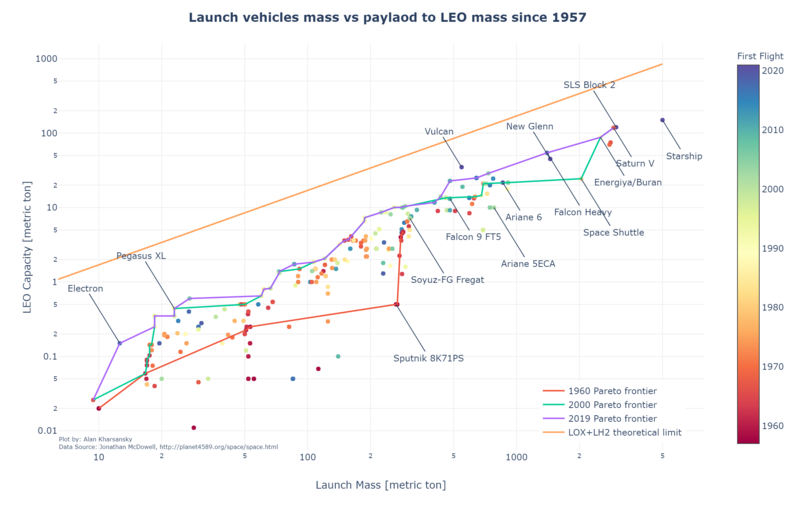
Useful payload to orbit is driven by the Rocket Equation and then affected by the different efficiency factors and non-idealities of the real Launch Vehicles designed and implementation. The trend in the payload to mass ratio is illustrated in the following plot using historical database <ref>McDowell's JSR Database (Links not working)</ref> since 1957. Only those LVs which has successfully achieved orbit at least once and carrying more than 10 Kg of payload were considered. A trend towards bigger LVs and more efficient can be observed.

Caveat: the LEO capacity figure is an approximation and is not normalized to a specific orbit across LVs. A substantial difference might be present if the stated LEO capacity was calculated for a 600 KM SSO orbit instead of a 400 Km equatorial orbit.

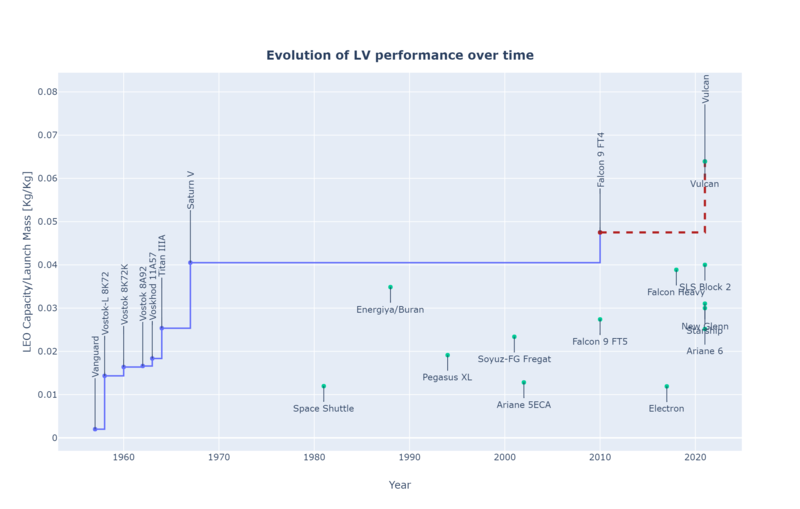
The evolution over time of this FOM can be seen in the following plot. In this case, only those LV that are better than the previous ones is plotted.

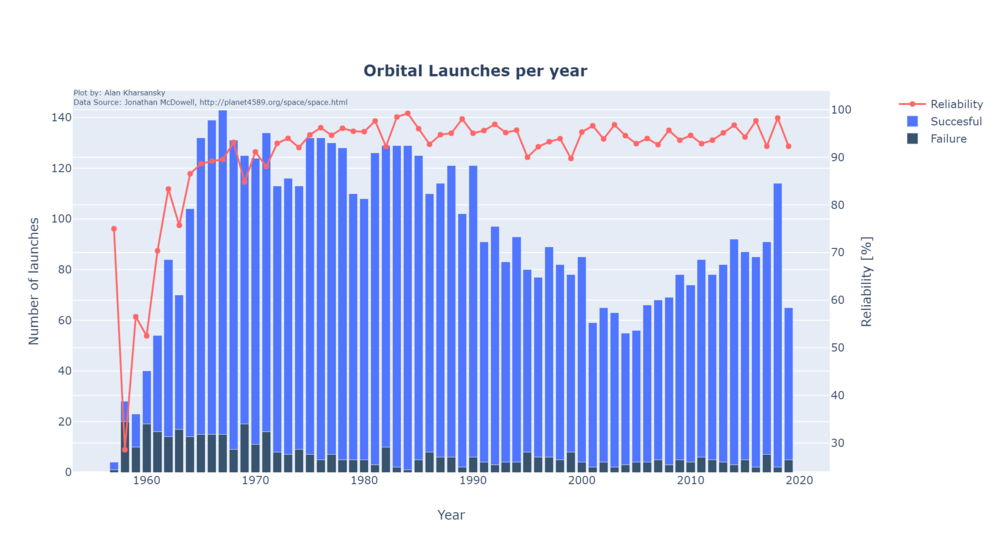
Payload to LEO [Kg/Year]

Put trends here

Reliability